複素数アプリを使う
複素数を使って計算するには、はじめに複素数アプリを起動します。
 を押し、複素数アイコンを選び、
を押し、複素数アイコンを選び、 を押してください。
を押してください。
複素数を入力する
複素数は、直交座標形式 (a+bi) または極座標形式 (r∠θ) で入力可能です。
例 1:2+3i を入力する
- 2
 3
3
 (i)*
(i)* 
* 「i」は、 – [複素数] > [i] と操作して入力することもできます。
– [複素数] > [i] と操作して入力することもできます。
例 2:5∠30 を入力する
- 5
 – [複素数] > [∠] 30
– [複素数] > [∠] 30 
複素数アプリの計算例
計算例の操作前に
下記の例題は、SETTINGS メニューの「入力/出力」の設定で「数学自然表示入出力」が選択されている状態で操作してください。その他の設定は、各例題の表示に従ってください。
複素数の計算結果は、SETTINGS メニューの「複素数結果表示」の設定に従って表示されます。
複素数を極座標形式で入力したり、計算結果を表示したりする場合は、計算を始める前にSETTINGS メニューの「角度単位」を設定してください。
計算結果の θ 値は、-180° < θ ≤ 180°の範囲で表示されます。
SETTINGSメニューの「入力/出力」の設定で「数学自然表示入出力」以外が選択されているとき、計算結果は a と bi(または r と θ)が別の行に表示されます。
例 3:(1 + i)4 + (1 - i)2 = -4 - 2i
(複素数結果表示:直交座標形式(a+bi))
 1
1

 (i)
(i)
 4
4

 1
1

 (i)
(i)

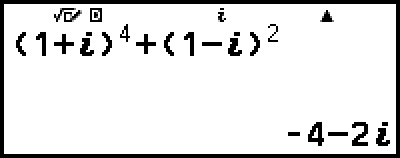
メモ
複素数の整数べき乗(a+bi)n は、-1 × 1010 < n < 1 × 1010 の範囲で可能です。
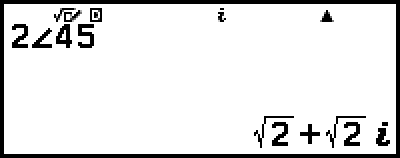
例 4:2∠45 = √2 + √2i
(角度単位:度数法(D)、複素数結果表示:直交座標形式(a+bi))
- 2
 – [複素数] > [∠] 45
– [複素数] > [∠] 45
例 5:√2 + √2i = 2∠45
(角度単位:度数法(D)、複素数結果表示:極座標形式(r∠θ))
 2
2

 2
2

 (i)
(i)

例 6:2 + 3i の共役複素数を求める
(複素数結果表示:直交座標形式(a+bi))
 – [複素数] > [共役複素数]
– [複素数] > [共役複素数]
2 3
3
 (i)
(i)

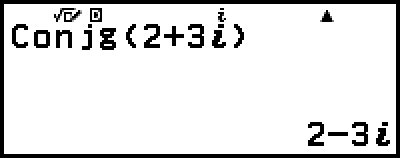
例 7:1 + i の絶対値と偏角を求める
(角度単位:度数法(D))
 – [数値計算] > [絶対値]
– [数値計算] > [絶対値]
1

 (i)
(i)

 – [複素数] > [偏角]
– [複素数] > [偏角]
1

 (i)
(i)


例 8:2 + 3i の実部と虚部を抽出する
 – [複素数] > [実部抽出]
– [複素数] > [実部抽出]
2 3
3
 (i)
(i)


 – [複素数] > [虚部抽出]
– [複素数] > [虚部抽出]
2 3
3
 (i)
(i)


複素数の計算結果を直交座標形式または極座標形式に変換する
 を押すと表示される FORMAT メニューを使って、複素数の計算結果を直交座標形式または極座標形式に変換できます。
を押すと表示される FORMAT メニューを使って、複素数の計算結果を直交座標形式または極座標形式に変換できます。
例 9:√2 + √2i = 2∠45, 2∠45 = √2 + √2i
(角度単位:度数法(D)、複素数結果表示:直交座標形式(a+bi))
 2
2

 2
2

 (i)
(i)

 – [極座標表示]
– [極座標表示]
 – [直交座標表示]
– [直交座標表示]
