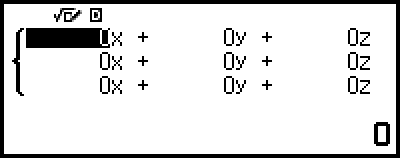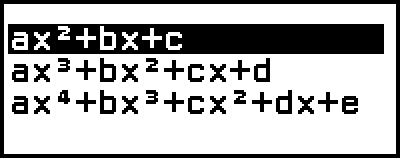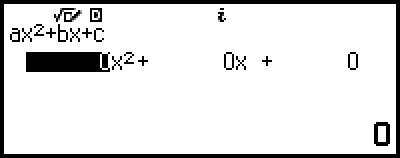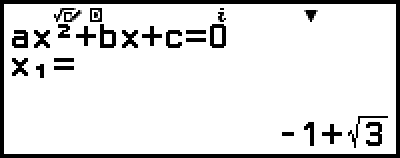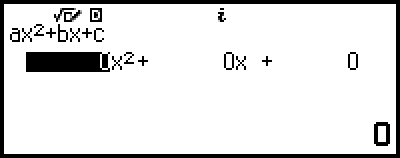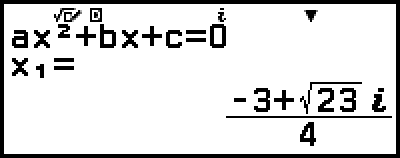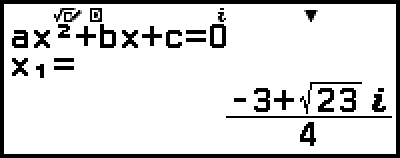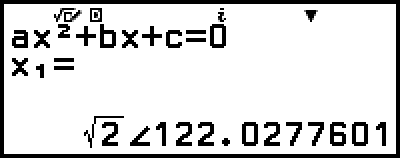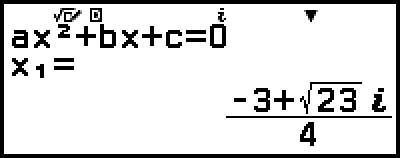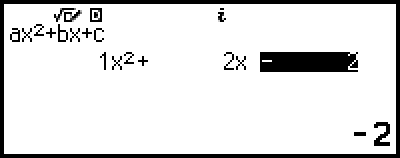方程式アプリを使う
方程式アプリには、下記3つの機能が含まれています。アプリを起動すると表示される方程式メニューから、使いたい機能を選びます。
連立方程式：2元～4元の連立方程式
高次方程式：2次～4次の高次方程式
ソルブ機能：入力した方程式に含まれる任意の変数の値を求める機能
連立方程式
ここでは本機で連立方程式を解くための一般的な操作を、3元連立方程式の例題で説明します。
例 1：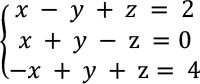
1. 
を押し、方程式アイコンを選び、
を押す。
方程式メニューが表示されます。
2. [連立方程式] を選び、を押す。
元数の選択メニューが表示されます。
3. [3元連立方程式] を選び、を押す。
係数エディターが表示されます。
4. 係数エディターを使って、係数値を入力する。
- 1
((-))112
11((-))10
((-))1114 
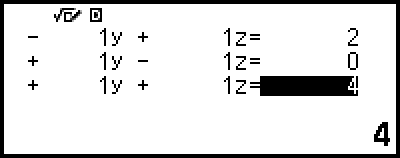
を押すと、すべての係数値が0になります。
5. を押す。
解が表示されます。
インジケーターが表示されているときは、
（または）を押すと別の解が表示されます。
- （または）
- （または）
インジケーターが表示されているときに
または
を押すと、1つ前に表示していた解が再表示されます。
最後の解が表示されているときにを押すと、係数エディターに戻ります。どの解が表示されているときでも、を押せば係数エディターに戻ります。
係数エディターの表示中にを押すと、元数の選択メニューに戻ります。
メモ
係数エディターの表示中は、現在反転しているカーソル位置の値を変数に保存できます。また、解の表示中は、その値を変数に保存できます。変数について詳しくは、「変数メモリー (A、B、C、D、E、F、x、y、z)」を参照してください。
高次方程式
方程式アプリで高次方程式を解くと、次数に応じて下記の値を表示します。
2次方程式の場合
ax2+bx+c=0 の解が表示され、続いて y=ax2+bx+c の最小値（または最大値）の座標（x, y）が表示されます。
3次方程式の場合
ax3+bx2+cx+d=0 の解が表示され、続いて y=ax3+bx2+cx+d の極小値（または極大値）の座標（x, y）が表示されます（極小値または極大値が存在する場合のみ）。存在しない場合は、最後の解の表示中にを押すと「極値をもたない」というメッセージが表示されます。
4次方程式の場合
ax4+bx3+cx2+dx+e=0 の解が表示されます。
ここでは2次方程式を例に、本機で高次方程式を解くための一般的な操作を説明します。
例 2：x2 + 2x − 2 = 0
（入力/出力：数学自然表示入出力）
1. を押し、方程式アイコンを選び、を押す。
方程式メニューが表示されます。
2. [高次方程式] を選び、を押す。
次数の選択メニューが表示されます。
3. [ax2+bx+c] を選び、を押す。
係数エディターが表示されます。
4. 係数エディターを使って、係数値を入力する。
- 12((-))2
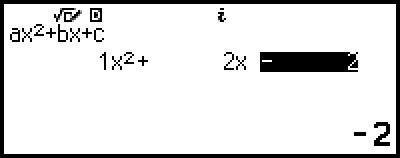
を押すと、すべての係数値が0になります。
5. を押す。
解が表示されます。
インジケーターが表示されているときは、（または）を押すと別の計算結果（解または座標値）が表示されます。
- （または）
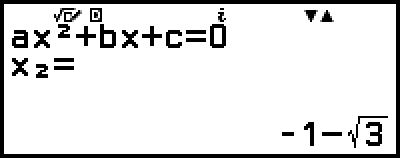
（y = x2 + 2x − 2 の最小値の x 座標を表示）
- （または）
（y = x2 + 2x − 2 の最小値の y 座標を表示）
- （または）
インジケーターが表示されているときにまたはを押すと、1つ前に表示していた計算結果が再表示されます。
最後の計算結果が表示されているときにを押すと、係数エディターに戻ります。どの計算結果が表示されているときでも、を押せば係数エディターに戻ります。
係数エディターの表示中にを押すと、次数の選択メニューに戻ります。
メモ
係数エディターの表示中は、現在反転しているカーソル位置の値を変数に保存できます。また、計算結果（解または座標）の表示中は、その値を変数に保存できます。変数について詳しくは、「変数メモリー (A、B、C、D、E、F、x、y、z)」を参照してください。
虚数結果の表示について（虚数結果表示）
高次方程式の解は、虚数となることがあります。方程式メニューから高次方程式を選んだときは、虚数結果を表示するかしないかの設定を、下記の操作で切り替えることができます。
– [虚数結果表示] > [する]
虚数結果を表示する設定に切り替わります（初期設定）。
– [虚数結果表示] > [しない]
虚数結果を表示しない設定に切り替わります。この設定のときに、虚数解しか持たない方程式を入力して計算すると、「実数解なし」というメッセージが表示されます。
例 3：2x2 + 3x + 4 = 0
（入力/出力：数学自然表示入出力、複素数結果表示：直交座標形式(a+bi)、虚数結果表示：する）
1. を押し、方程式アイコンを選び、を押す。
方程式メニューが表示されます。
2. [高次方程式] > [ax2+bx+c] を選ぶ。
係数エディターが表示されます。
3. 係数エディターを使って、係数値を入力する。
- 234
4. を押す。
解が表示されます。
5. 別の解や座標値を表示する。
- （または ）
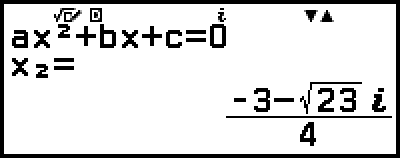
- （または）
- （または）
最後の計算結果が表示されているときにを押すと、係数エディターに戻ります。どの計算結果が表示されているときでも、を押せば係数エディターに戻ります。
方程式の虚数解を直交座標形式または極座標形式に変換する
を押すと表示される FORMAT メニューを使って、虚数解を直交座標形式または極座標形式に変換できます。
例 4：例3で表示された虚数解を極座標形式に変換し、続いて直交座標形式に変換する
1. 例3の手順1～4を実行する。
2. を押し、[極座標表示] を選び、を押す。
解が極座標形式に変換されます。
3. を押し、[直交座標表示] を選び、を押す。
解が直交座標形式に変換されます。
ソルブ機能
ソルブ機能は、方程式の解をニュートン法で近似的に求める機能です。下記のような式を入力して、解を求めることができます。
例：y = x + 5、x = sin(A)、xy + C（xy + C = 0と扱われます）
例 5：x2 - B2 = 0 を x について解く（B = 4とする）
（入力/出力：数学自然表示入出力）
メモ
x2 - B2 = 0 を x について解く前に、変数 B に4を保存する必要があります。この操作は下記手順3で実行します。
1. を押し、方程式アイコンを選び、を押す。
方程式メニューが表示されます。
2. [ソルブ機能] を選び、を押す。
ソルブ機能の式入力画面が表示されます。
3. ここで、変数 B に4を保存する。
4
この操作は、手順7以前であればいつ実行しても構いません。
変数について詳しくは、「変数メモリー (A、B、C、D、E、F、x、y、z)」を参照してください。
ソルブ機能の式入力画面に戻るには、を押します。
4. 式を入力する。
(B)
2
(=)*0
* 「=」記号は、
– [方程式] > [=] と操作して入力することもできます。
5. を押して、入力した式を確定する。
6. 表示される「求めたい変数を選択して下さい」画面で [x] が選択されているのを確認し、を押す。
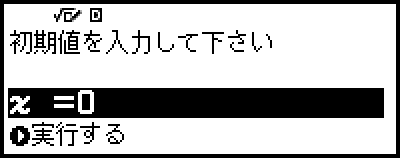
x の初期値を入力する画面が表示されます。
7. x の初期値として1を入力する。
- 1
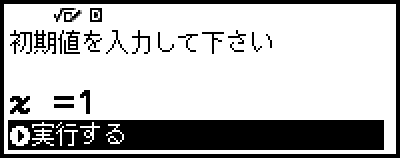
8. [実行する] が選択されているのを確認し、を押して解を表示する。
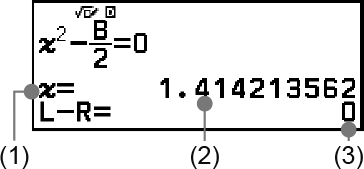
(1) 求解対象の変数
(2) 解
(3) (左辺) − (右辺)の結果
解は常に小数で表示されます。
解の精度は、(左辺) − (右辺) の結果が0に近いほど高くなります。
9. 次にしたい操作に応じたキーを押す。
| これをしたいときは： | このキーを押す： |
|---|---|
| 手順6の画面に戻る | * |
| 手順4の画面に戻る（入力式は保持されます） | または |
* このキーを押したとき、x の初期値は計算で最後に使われた初期値となります。
重要
-
ソルブ機能は解の収束に向けて決まった回数の計算を実施します。もし求解できなかった場合は、計算を継続するかどうか確認する画面が表示されます。計算を継続するには [継続する] を、終了するには [終了する] を選び、
を押してください。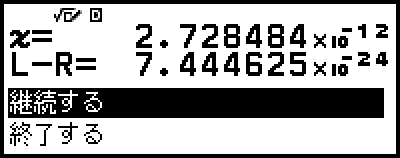 
求解対象の変数（上記例題では x）に代入した初期値によっては、ソルブ機能で解を求めることができない場合があります。この場合、初期値をより解に近いと思われる値に変更し、再度計算してください。
解が存在する式でも、ソルブ機能では求解できない場合があります。
ソルブ機能はニュートン法を使って計算するため、複数の解が存在する場合でも、そのうち1つの解だけを返します。
ニュートン法の性質上、y=sinx、y=ex、y=√x などのような関数は、解を求めにくい傾向にあります。
方程式アプリで真偽判別を使う
方程式アプリでは、連立方程式または高次方程式で真偽判別を使うことができます。方程式アプリで真偽判別を有効にすると、解が表示される代わりに、下記のような回答メニューが表示されます。
このメニューを使って回答する（[解を入力する] を選んで解を入力するか、[解なし] または [無数の解] を選ぶ）と、本機はその回答の真偽を判別します。
メモ
上記のメニューは、連立方程式で表示されるものです。高次方程式では、メニューの内容が異なります。
真偽判別は、本機のいくつかの電卓アプリで利用できる機能です。ここでの操作前に、「真偽判別の概要」をお読みください。
真偽判別は、方程式アプリの下記機能では使えません。
- [連立方程式] > [3元連立方程式] または [4元連立方程式]
- [高次方程式] > [ax3+bx2+cx+d] または [ax4+bx3+cx2+dx+e]
- [ソルブ機能]
真偽判別が有効のときに方程式メニューから上記いずれかのメニュー項目を選ぶと、「真偽判別は非対応です」というメッセージが表示されます。
真偽判別の操作例
例 6：例2で解いた方程式 x2 + 2x - 2 = 0 の2つの解（x1 = -1 + √3、x2 = -1 - √3）を入力し、真偽を判別する。さらに、この方程式が最小値と最大値のどちらを持つかを選び、その座標値（x, y）を入力し、真偽を判別する。
1. 例2の手順1～4を実行する。
2. 真偽判別を有効にするには、を押し、[真偽判別を有効化] を選ぶ。
真偽判別が有効になったことを表す
インジケーターが、画面上部に表示されます。
3. を押す。
2次方程式の回答メニューが表示されます。
4. [解] が選択されているのを確認し、を押す。
解の個数を選ぶメニューが表示されます。
5. ここでは [解は2個] を選び、を押す。
6. 表示される解の入力画面で、x1 と x2 を入力する。
- ((-))1
3
((-))13 
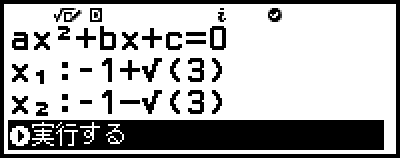
7. [実行する] が選択されているのを確認し、を押す。
解の個数と、入力した解がすべて正しいときは、「真」と表示されます。
解の個数、または入力した解に誤りがあるときは、「偽」と表示されます。またはを押して解の入力画面に戻り、数値を入力し直してください。解の個数を選び直したいときは、解の入力画面でを押し、手順4からやり直してください。
8. [方程式入力画面に戻る] が選択されているのを確認し、を押す。
手順1の係数エディターに戻ります。
9. を押して回答メニューを表示し、[最大値] または [最小値] を選ぶ。
方程式 x2 + 2x - 2 = 0 は最小値を持つので、ここでは [最小値] を選び、を押します。
10. 表示される座標値の入力画面で、x と y を入力する。
- ((-))1
((-))3 
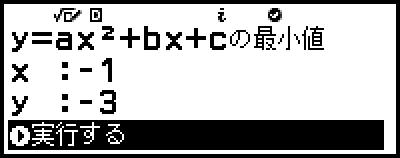
11. [実行する] が選択されているのを確認し、を押す。
最大値または最小値の選択と、入力した座標値がすべて正しいときは、「真」と表示されます。
最大値または最小値の選択、または入力した座標値に誤りがあるときは、「偽」と表示されます。またはを押して座標値の入力画面に戻り、数値を入力し直してください。最大値または最小値を選び直したいときは、座標値の入力画面でを押し、手順9からやり直してください。
12. [方程式入力画面に戻る] が選択されているのを確認し、を押す。
手順1の係数エディターに戻ります。
13. 真偽判別の操作を終了するには、を押し、[真偽判別を無効化] を選ぶ。
インジケーターが消えます。
真偽判別を無効にする操作について詳しくは、「真偽判別を無効にするには」を参照してください。
メモ
手順8または手順12で [解を確認する] を選んでを押すと、解および最小値を確認できます。表示される画面と可能な操作は、例2の手順5と同じです。
