Equationアプリ(方程式)
Equationアプリは、連立一次方程式(2元~6元)や高次方程式(2次~6次)を解くことができます。また、方程式を任意の変数について解くSolver機能を備えています。
連立一次方程式を解く
例: の、を求める
-
h > Equationを選ぶ。
-
Typeタブで[Simultaneous]を選び、>またはOを押す。
-
Unknownsタブで未知数の数を選び、>またはOを押す。
-
表示されるEditorタブで、方程式の係数を入力する。
-
解を求めるには、>またはOを押す。
ここでは未知数が、の2つなので、[2 Unknowns]を選びます。
2Es-(M)1E5E
1E2E10E
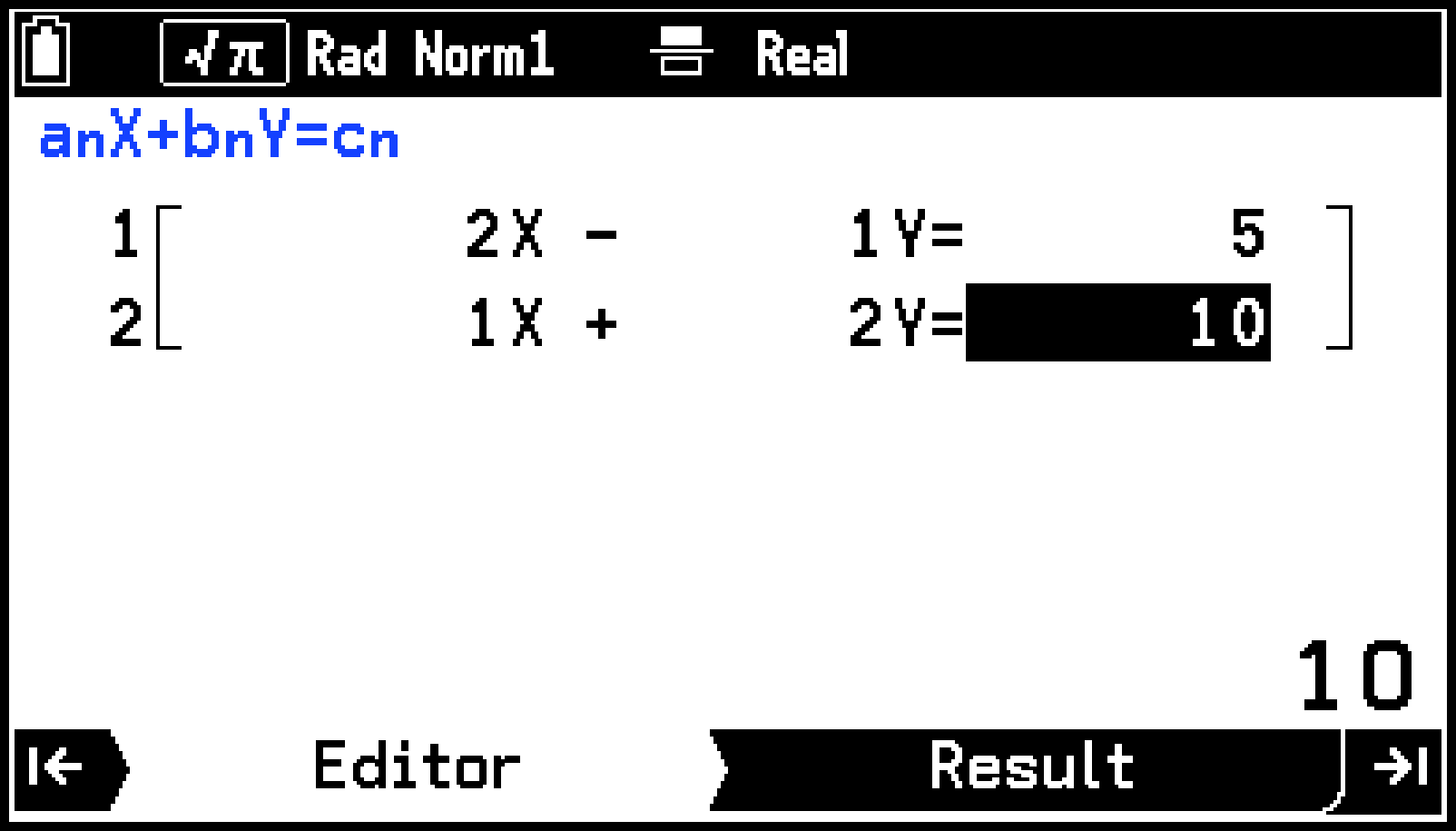
Resultタブに、の解が表示されます。カーソル位置のセル内の数値が、ウインドウ右下に詳細表示されます。*
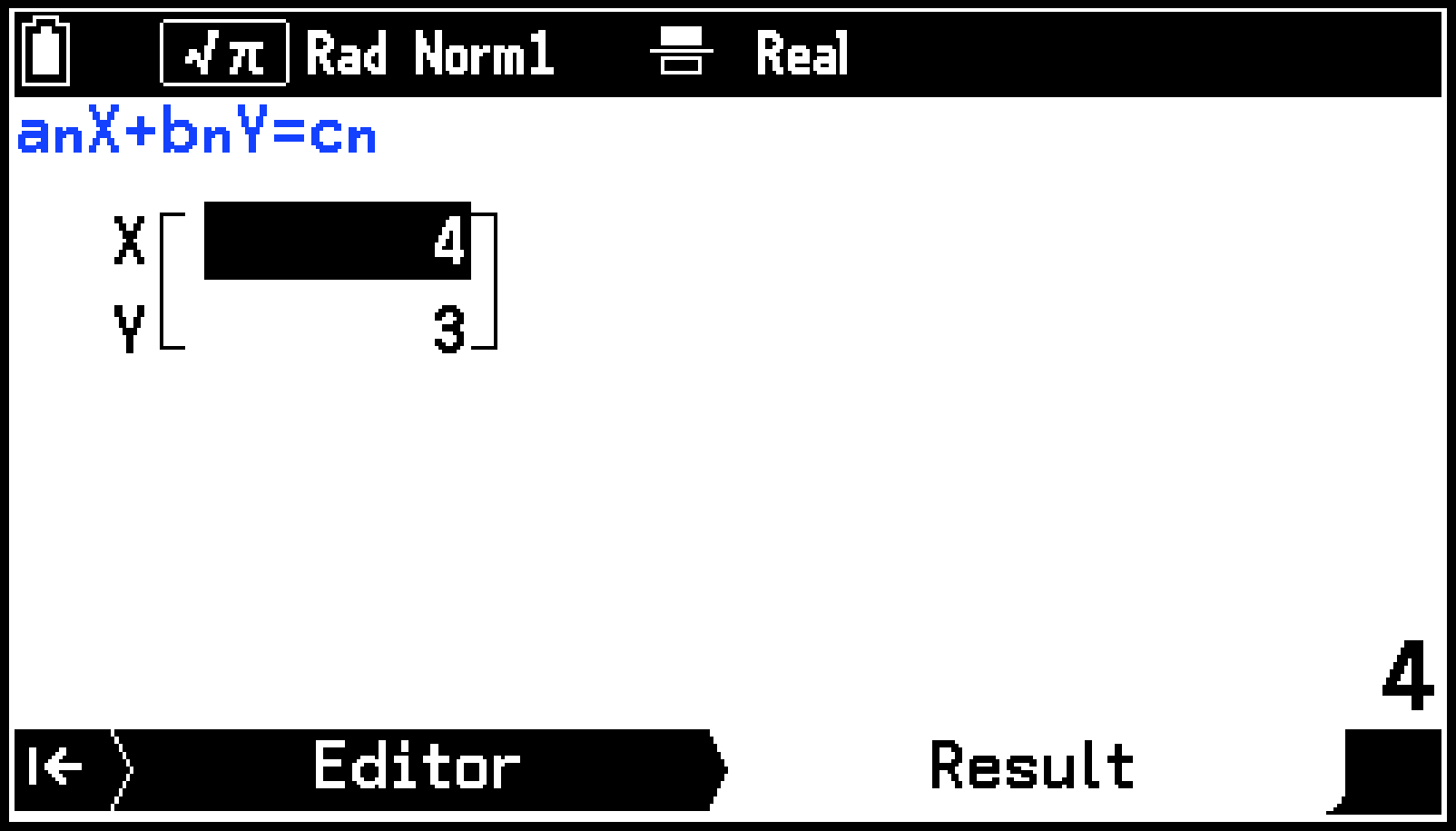
S > [ Result]がオンのとき、可能な場合はやを含む形式で表示されます(可能でない場合は小数形式となります)。
S > [ Result]がオフのときは、小数形式のみで表示されます。
参考
解が無数にある場合は“Infinitely Many Solutions”と表示されます。
本機は連立一次方程式の解を、係数行列の逆行列-1を用いて求めています。このため係数行列の行列式Det()が0に近づくと、精度が落ちる場合があります。
高次方程式を解く
例: を解く
-
h > Equationを選ぶ。
-
Typeタブで[Polynomial]を選び、>またはOを押す。
-
Degreeタブで次数を選び、>またはOを押す。
-
表示されるEditorタブで、方程式の係数を入力する。
-
解を求めるには、>またはOを押す。
ここでは2次方程式を解くので、[a2X2+a1X+a0=0]を選びます。
1E2Es-(M)2E
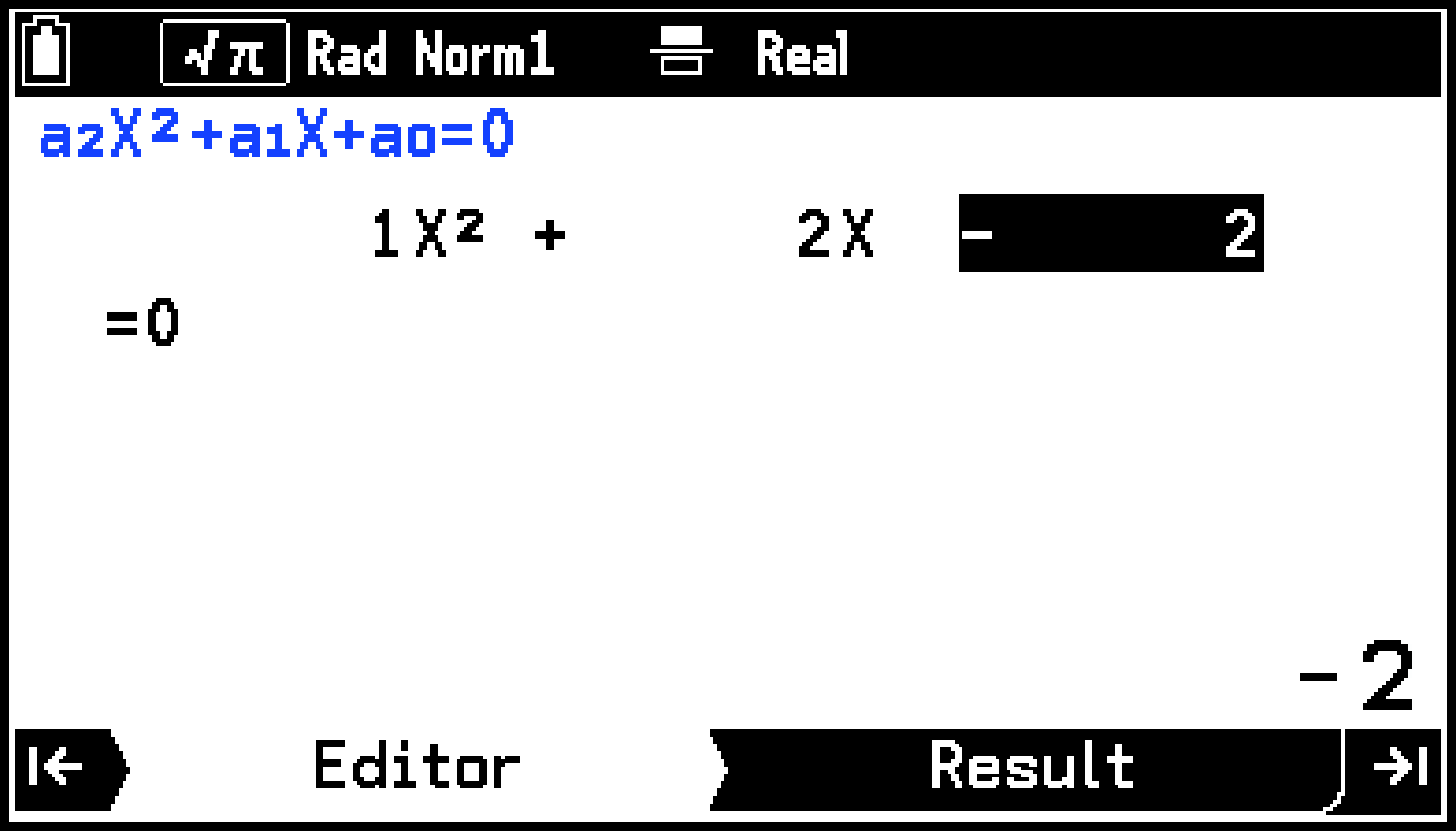
Resultタブにの解が表示されます。カーソル位置のセル内の数値が、ウインドウ右下に詳細表示されます。*
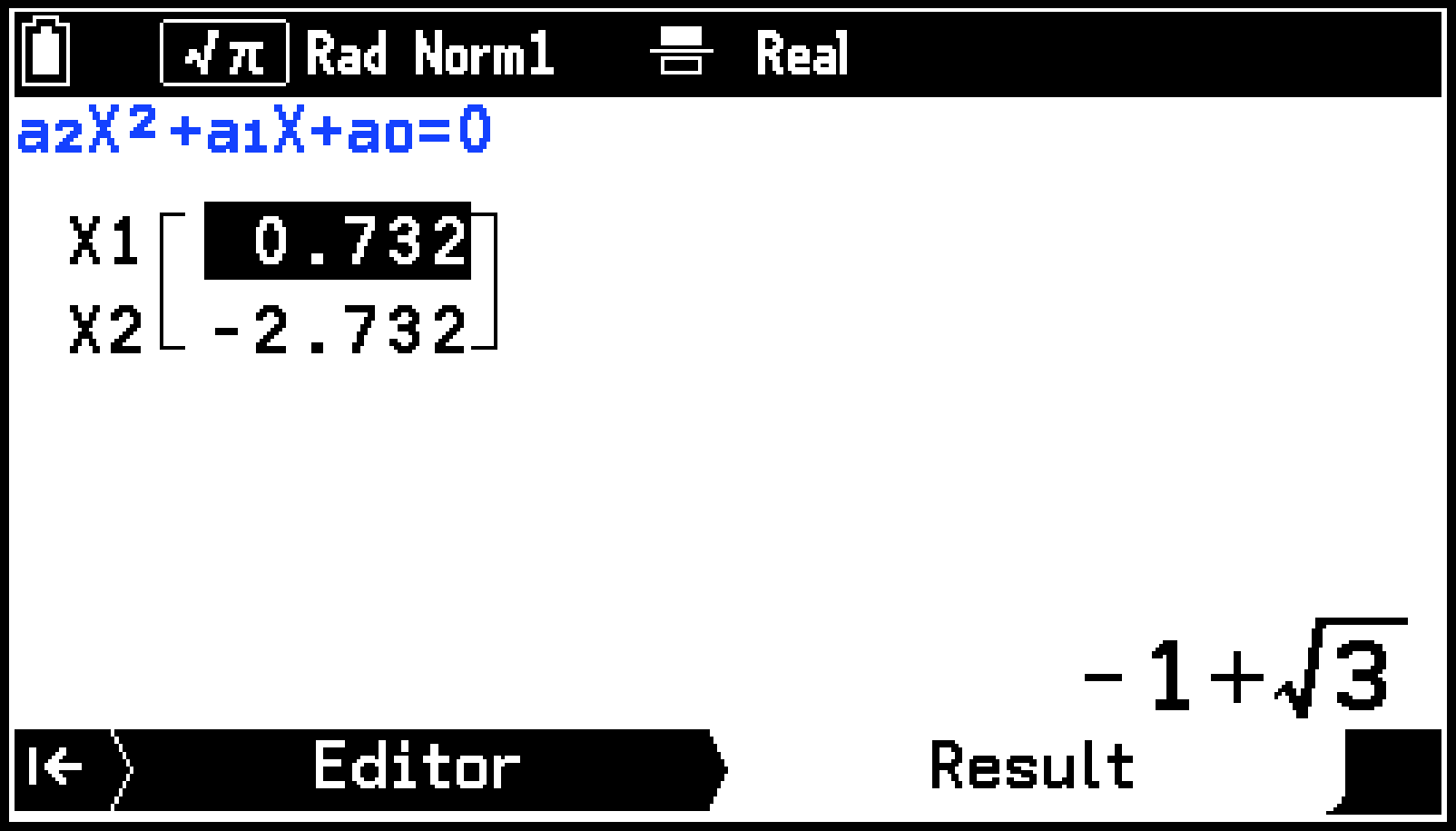
S > [ Result]がオンのとき、可能な場合はやを含む形式で表示されます(可能でない場合は小数形式となります)。
S > [ Result]がオフのときは、小数形式のみで表示されます。
参考
方程式が重解を持つ場合、その個数が解の右側に表示されます。
例: の解

なお方程式によってはごく稀に、重解の計算結果表示が不正確になったり、エラーとなったりすることがあります。
方程式が虚数解を持つ場合、解はS > [Complex Mode]の設定に応じた形式で表示されます。
ResultタブではSキーの操作は無効です。Editorタブで操作してください。
Solverを使う
式の変形や整理など方程式を解く手間を省いて、その方程式に含まれる任意の変数の値を求めることができます。
例: ある物体が空気中に初速Vで投げ出され、T時間後に高さHに到達したとする。次の式を使って、H=14(m)、T=2(秒)、重力加速度G=9.8(m/s2)の場合の初速Vを求めよ。
-
h > Equationを選ぶ。
-
Typeタブで[Solver]を選び、>またはOを押す。
-
SetupタブのEq行に、方程式をそのままの形で入力する。
-
Oを押す。
-
方程式をどの変数について解くか指定する。
-
Oを押してSolve forダイアログを表示する。
-
初速Vを求めるので[V]を選び、Oを押す。
-
H=14、T=2、G=9.8を順次入力する。
-
>を押す。または、
 を反転させOを押す。
を反転させOを押す。
H = VT -e1d2r GT i
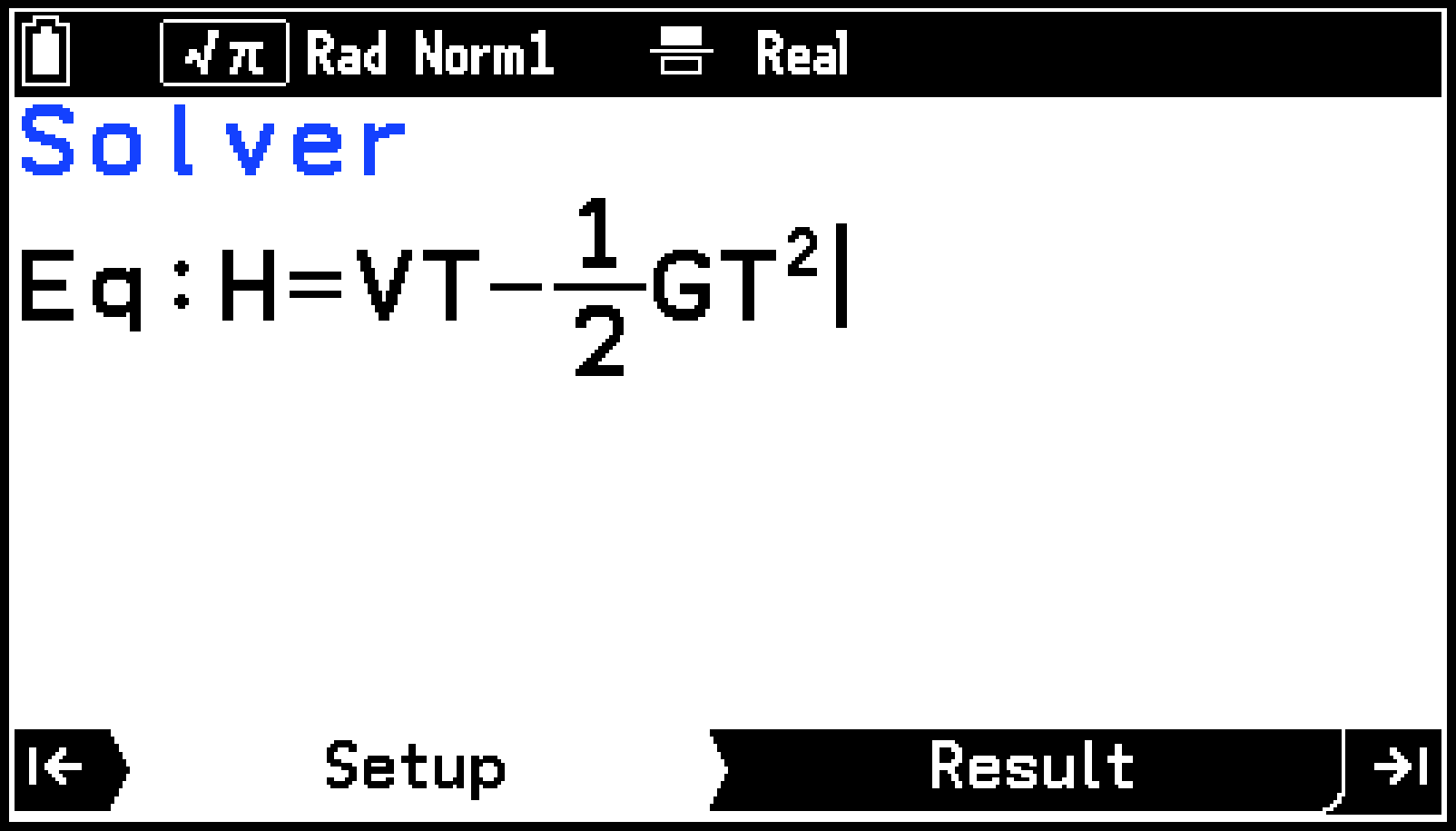
方程式の中に含まれている変数の一覧が表示されます。
14E0E*2E9.8E
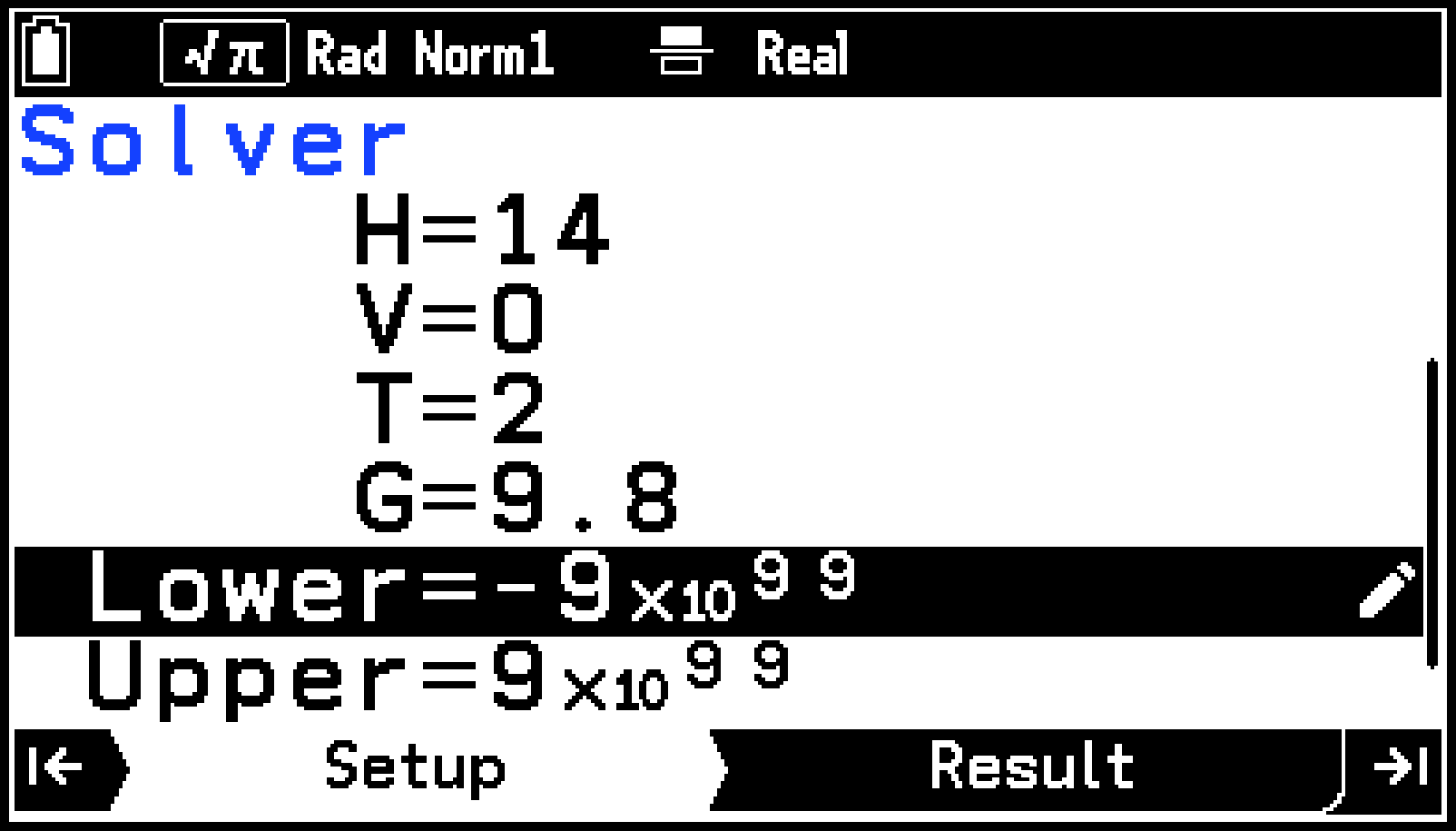
求解対象の初期推定値です。ここでは、初期推定値を0とします。
“Upper=”と“Lower=”の行には、必要に応じて求める解の上限値と下限値を入力します。
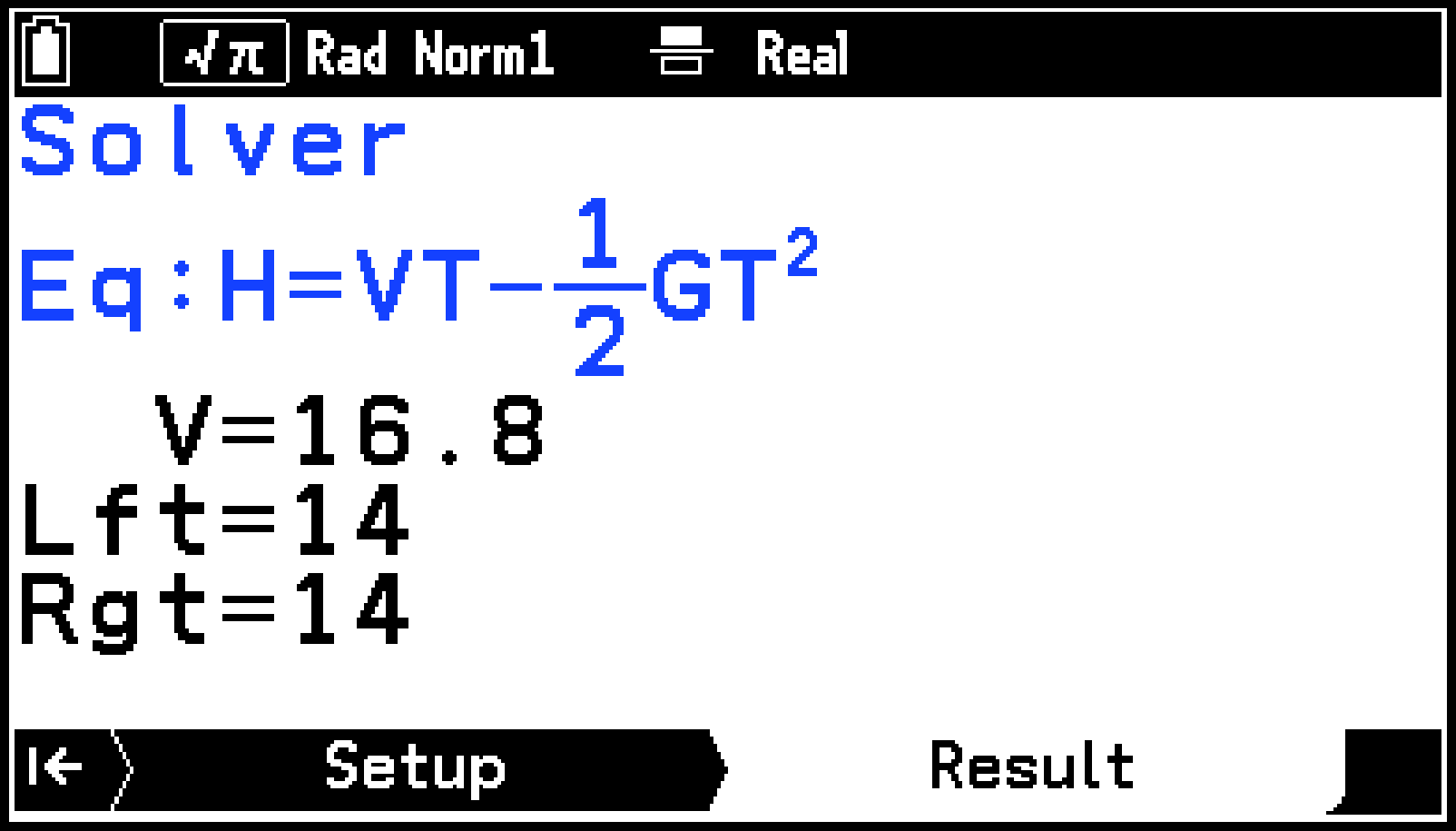
Resultタブに計算結果が表示されます。
“Lft=”と“Rgt=”は、求めた解で左辺と右辺を計算した結果を表します。
参考
とXは同じ変数として扱われます。
手順3の“Eq”行に“=”を含まない式を入力すると、“式 = 0”とみなされます。
Graph&Tableアプリで保存した関数式を、“Eq”行に入力できます。T > [Recall]を選び、入力したい関数式を反転させ、Oを押してください。
Solverは、ニュートン法を使った近似計算で解を求めます。“Lft=”と“Rgt=”の値が表示されるのは、ニュートン法による計算が真の解に対して誤差を生じる場合があるためです。“Lft=”と“Rgt=”の値の差が0に近いほど、計算結果の誤差が小さいことを表します。
表示された解の収束が十分でない場合、![]() ボタンが表示されます。
ボタンが表示されます。
Solverでは、解は1つだけが求められます。高次方程式(など)の複数の解を求めたいときは、高次方程式を解くを参照してください。