> 各種情報 > Catalogメニュー詳細

Catalogメニュー詳細

Cを押すと表示されるCatalogメニューは、すべての関数・コマンド・アプリデータ変数^*・記号を包括した一覧です。このメニューから希望する項目を選んで、計算や式に入力できます。

C > [All]には、本機搭載の全項目が含まれます。アルファベット一覧の表示中にX^A～0^Zを押すと、押したキーのアルファベットから始まる先頭の項目にジャンプします。

[A]～[Z]に含まれない関数や記号は、C > [All] > [Symbol]に入っています。

C > [Variable Data]に含まれる項目です（アプリ内で使われる入出力用の変数）。

参考

PythonアプリとBase-NアプリでCを押すと、それぞれアプリ専用のCatalogメニューが表示されます。詳しくは、各アプリの章を参照してください。

Catalogメニューの表示は、カテゴリー別のメニューでは関数やコマンドの名称（例：Integration‎ (∫)‎など）、C > [All]および入力履歴のメニュー上では関数やコマンドのライン入力構文（例： “∫(,,)” など）で表示されます。

入力履歴を利用する

Catalogメニューから最近入力した関数やコマンドが10個まで^*、入力履歴として保持されます。入力履歴を表示するには、C > [History (Pin ‎ Pin )‎]を選びます。

ピン留めした入力履歴を含みます。

入力履歴をピン留めする

入力履歴の表示中に、ピン留めしたい項目を選び、Tを押します。項目の左側にピンが表示されます

ピン留めした項目は、次回入力履歴を開いたとき、先頭に移動します。

ピン留めを解除するには、解除したい項目の行を選び、Tを押します。

カテゴリー別項目一覧

Unit Conversions（単位換算）カテゴリーを除く関数やコマンドの構文は、下記の要領で記述しています。

自然入力とライン入力で構文が異なる場合は、自然入力、ライン入力の順に記載しています。

構文中で入力を省略してよい範囲は、[ ] で括っています。例えば $∫ (f (x), a, b [, t o l])$ という構文は、引数の $t o l$ を省略して $∫ (f (x), a, b)$ の形で使うことができます。

参考

本節に記載されているカテゴリーと、各カテゴリーに含まれる関数・コマンド・アプリデータ変数^*・記号は、Systemアプリで[Country] > [International]を選んだときの表示順、表示項目となっています。

設定に関わらず、C > [All]に含まれている項目は同じです。本書に掲載されている全項目が、アルファベット順に表示されます。

C > [Variable Data]に含まれる項目です（アプリ内で使われる入出力用の変数）。

Function Analysis（解析関数）

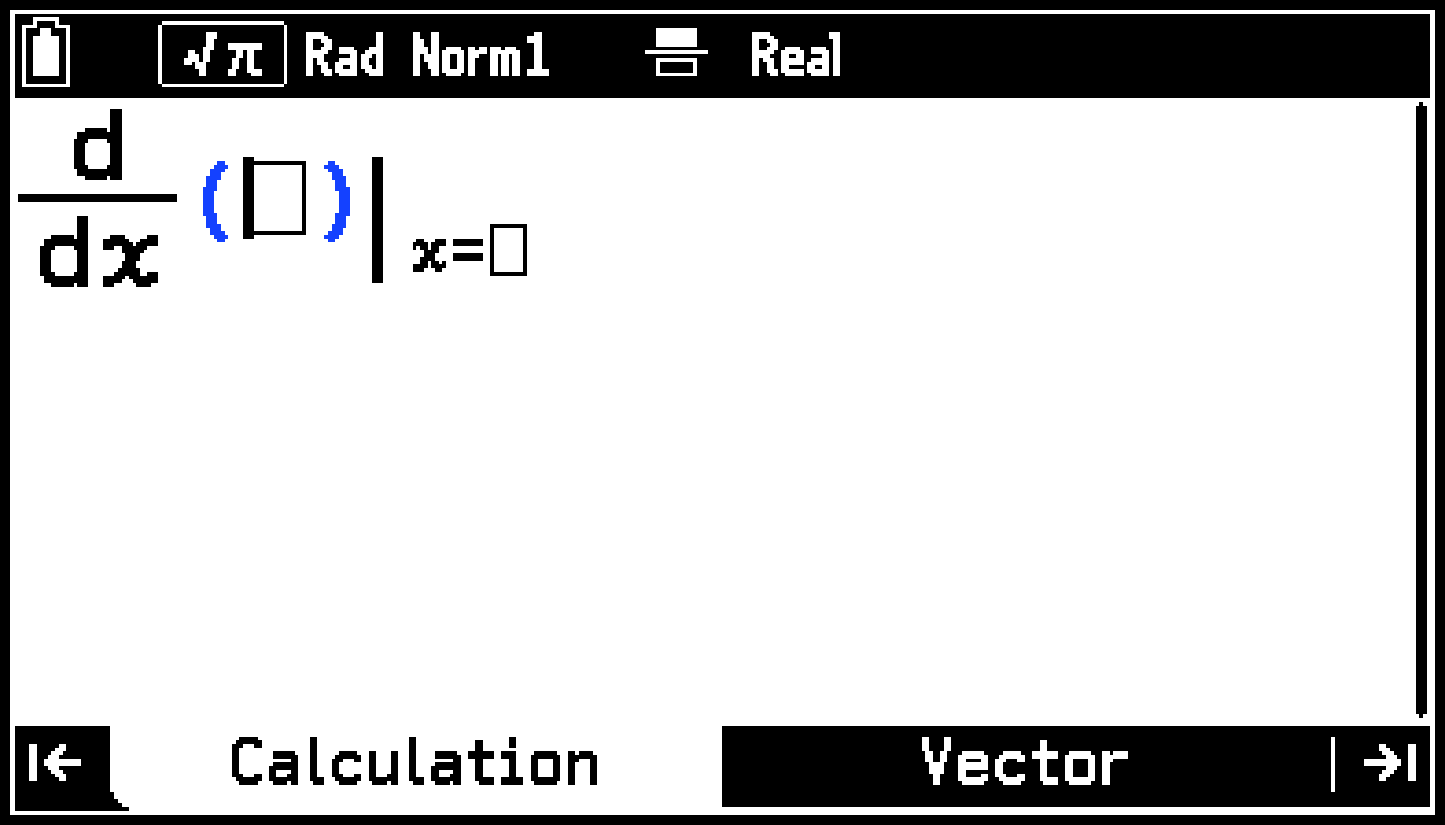
1st Derivative‎ (d/dx) d/dx(,)

$f (x)$ の $x = a$ における1次微分係数を、近似計算により求めます。

構文： $\frac{d}{d x} (f (x)) |_{x = a}$ $d / d x (f (x), a)$

構文内では使用不可： $d / d x$ 、 $d^{2} / d x^{2}$ 、 $∫ d x$ 、Σ、FMin、FMax、Solve、RndFix

例: $\frac{d}{d x} (f (x^{3} + 4 x^{2} + x - 6)) |_{x = 3} = 52$

注意事項

$f (x)$ が三角関数の場合、必ずS > [Angle] > [Radian]を選択してください。

次の場合は、計算結果の精度が落ちたり、エラーが発生したりします。

$x$ 値における不連続な点

$x$ 値における極端な変化

$x$ 値における極大点や極小点の含有

$x$ 値における変曲点の含有

$x$ 値における1 次微分不可能点の含有

計算結果がゼロに近づく

2nd Derivative‎ (d²/dx²) d²/dx²(,)

$f (x)$ の $x = a$ における2次微分係数を、近似計算により求めます。

構文： $\frac{d^{2}}{{d x}^{2}} (f (x)) |_{x = a}$ $d^{2} / {d x}^{2} (f (x), a)$

「構文内では使用不可」と「注意事項」は、 $d / d x$ と同様です。

Integration‎ (∫)‎ ∫(,,)

$f (x)$ の $a$ ≤ $x$ ≤ $b$ における積分値を、近似計算により求めます。この関数は、 $f (x)$ が正の範囲では正の値、負の範囲では負の値を返します（例： $∫_{2}^{3} x^{2} - 4 d x = \frac{7}{3}$ ； $∫_{1}^{2} x^{2} - 4 d x = - \frac{5}{3}$ ）。

構文： $∫_{a}^{b} f (x) d x$ $∫ (f (x), a, b [, t o l])$

$t o l$ には許容誤差範囲を入力します。省略時、および自然入力時は1×10^-5となります。

構文内では使用不可： $d / d x$ 、 $d^{2} / d x^{2}$ 、 $∫ d x$ 、Σ、FMin、FMax、Solve、RndFix

例: $∫_{1}^{5} {2 x}^{2} + 3 x + 4 d x = \frac{404}{3}$

注意事項

$f (x)$ が三角関数の場合、必ずS > [Angle] > [Radian]を選択してください。

積分計算では、 $f (x)$ の内容、積分区間における正・負、または積分したい区間によっては、計算結果の積分値に大きな誤差が生じることがあります（例えば積分区間に不連続な点や急激に変化する部分を含む場合、積分区間が広すぎる場合など）。このような場合、積分区間を分割して計算することで、計算精度が改善することがあります。

Summation‎ (Σ) Σ(,,,)

$f (x)$ について指定した範囲の総和を求めます。

構文： $\sum_{x = a}^{b} (f (x))$ $\sum (f (x), x, a, b [, n])$ $a$ , $b$ , $n$ は整数、 $a$ < $b$

$x$ には任意のアルファ変数を指定できます。 $n$ にはステップ値（ $a$ と $b$ の間隔）を指定します。省略時、および自然入力時は1となります。

構文内では使用不可： $d / d x$ 、 $d^{2} / d x^{2}$ 、 $∫ d x$ 、Σ、FMin、FMax、Solve、RndFix

例: $\sum_{x = 2}^{6} (x^{2} - 3 x + 5) = 55$

Solve Equation (SolveN) SolveN()

方程式の複数の解を一度に求めます。

構文： SolveN ( $f (x)$ [=右辺] [, $x$ ] [,下限,上限])

[=右辺]を省略すると、 $f (x)$ = 0として扱われます。[ $, x$ ]には任意のアルファ変数を指定し、同じ変数を $f (x)$ に使用します。[, $x$ ]を省略した場合の変数は、 $x$ となります。

最大10個までの解が、リスト形式で返されます。

解が存在しない場合は“No Solution”が返されます。

表示した解以外の解が存在する可能性があるときは、“More solutions may exist.‎ ”と表示されます。

構文内では使用不可： $d^{2} / d x^{2}$ 、Σ、FMin、FMax、Solve

例: SolveN $(x^{2} - 5 x - 6) = {- 1, 6}$

Solve Equation (Solve) Solve(,)

$f (x)$ = 0の1つの解を近似的に求めます。EquationアプリのSolverと同じ機能の関数です（Solverを使うを参照）。

構文： Solve ( $f (x)$ ,初期推定値[,下限,上限])

構文内では使用不可： $d^{2} / d x^{2}$ 、Σ、FMin、FMax、Solve

Remainder of Integer‎÷‎Integer Rmdr

整数を整数で割ったときの余りを求めます。

構文：割られる数 Rmdr 割る数

例: 17 Rmdr 7 = 3

Integer Part of Int‎÷‎Int Int÷

整数を整数で割ったときの商を求めます。

構文：割られる数 Int÷ 割る数

例: 17 Int÷ 7 = 2

Simplification ISimp

分数を約分します。Calculateアプリで、下記のとおりに設定して使用します。

S > [Simplify] > [Manual]

S > [Complex Mode] > [Real]

ISimpは下記いずれかの構文で使います。

構文1：分数 ISimp

引数の分数を、約分可能な最小の素数で自動的に約分します。約分に使った素数と約分の結果が表示されます。

構文2：分数 ISimp $n$

引数の分数を、指定した約数 $n$ によって約分します。

例 1: $\frac{15}{60} = \frac{5}{20} = \frac{1}{4}$

15e60r
C > [Function Analysis] > [Simplification]E

CY875_Function Analysis_Simplification_1

C > [History (Pin ‎ Pin )‎] > [ISimp]E

CY875_Function Analysis_Simplification_2

例 2: $\frac{15}{60} = \frac{3}{12}$ （約数5を指定）

15e60r
C > [Function Analysis] > [Simplification]5E

CY875_Function Analysis_Simplification_3

注意事項

S > [Complex Mode]の設定が[a‎+‎b‎ $i$ ‎]または[r‎∠‎θ‎]の場合、S > [Simplify] > [Manual]が選ばれていても、分数計算の結果は常に約分されて表示されます。

Function Minimum FMin(,,)

$f (x)$ の $a$ ≤ $x$ ≤ $b$ における最小値の座標をリスト形式で返します。

構文：FMin( $f (x)$ , $a$ , $b$ [, $n$ ]) $n$ : 計算精度（ $n$ は1～9の整数）

構文内では使用不可： $d / d x$ 、 $d^{2} / d x^{2}$ 、 $∫ d x$ 、Σ、FMin、FMax、Solve、RndFix

例: FMin( $x^{2}$ ,-2,1) = {0,0}

注意事項

不連続な点、急激に変化する部分では精度がでなかったり、エラーになったりすることがあります。

$n$ の数値を大きくすると精度が上がりますが、計算に要する時間は長くなります。

Function Maximum FMax(,,)

$f (x)$ の $a$ ≤ $x$ ≤ $b$ における最大値の座標をリスト形式で返します。

構文：FMax( $f (x)$ , $a$ , $b$ [, $n$ ]) $n$ : 計算精度（ $n$ は1～9の整数）

「構文内では使用不可」と「注意事項」は、FMinと同様です。

Probability（確率）

Factorial (!)‎ !

0または正の整数の階乗を求めます。

構文： $n!$ $n$ は整数

Permutation‎ (P) P

$n$ 個から $r$ 個を取り出す順列の総数を求めます。

構文： $n$ P $r$ $n$ 、 $r$ は整数

Combination‎ (C) C

$n$ 個から $r$ 個を取り出す組み合わせの総数を求めます。

構文： $n$ C $r$ $n$ 、 $r$ は整数

Random Number (0 to 1) Ran#

実行するたびに、0以上1未満の10桁の乱数1つを返します。

構文：　Ran# [ $a$ ] 1 ≤ $a$ ≤ 9 ( $a$ は整数)

$a$ ：乱数の系列を指定します。省略すると、ランダムな乱数が返されます。指定すると、指定に応じて本機が内蔵している9つの「系列乱数」の1つが呼び出され、決まった乱数が返されます。例えば系列の初期化後^*にRan# 1を実行すると、先頭から順番に0.701320948、0.9297706456、0.2939058016、…という系列1の乱数が必ず返されます。

系列を初期化するには、Ran# 0を実行します。このとき、RanList#の系列も同時に初期化されます。また、Ran#またはRanList#を使って直前に実行した系列とは異なる系列の乱数を発生させたり、ランダムな乱数を発生させたりすると、系列は初期化されます。

Random Integer (n to m) RanInt#(,)

指定した2つの整数 $n$ 、 $m$ の間の整数乱数を発生します。

構文：　RanInt#( $n$ , $m$ [, $a$ ]) $n$ < $m$ 、| $n$ | < 1×10¹⁰、| $m$ | < 1×10¹⁰、 $m$ ‒ $n$ < 1×10¹⁰、1 ≤ $a$ ≤ 999

$a$ ：乱数の個数を指定します。省略すると乱数1つを返します。指定すると、その個数の乱数をリスト形式で返します。

Random Number (Normal) RanNorm#(,)

指定した平均 $μ$ と標準偏差 $σ$ の値に基づき、正規分布に従って10桁の乱数を発生します。

構文： RanNorm#( $σ$ , $μ$ [, $n$ ]) $σ$ > 0、1 ≤ $n$ ≤ 999

$n$ ：乱数の個数を指定します。省略すると乱数1つを返します。指定すると、その個数の乱数をリスト形式で返します。

例: 1歳未満の子供の平均身長が68cm、標準偏差が8のとき、正規分布に従って身長が取り得る値の乱数を発生させる： RanNorm#(8,68)

Random Number (Binomial) RanBin#(,)

指定した試行回数 $n$ と確率 $p$ の値に基づく2項分布に従って、整数の乱数を発生します。

構文： RanBin#( $n$ , $p$ [, $m$ ]) 1 ≤ $n$ ≤ 100000、1 ≤ $m$ ≤ 999、0 ≤ $p$ ≤ 1

$m$ ：乱数の個数を指定します。省略すると乱数1つを返します。指定すると、その個数の乱数をリスト形式で返します。

Random Num (0 to 1) to List RanList#()

実行するたびに、指定した個数の乱数（0以上1未満、10桁）をリスト形式で返します。

構文： RanList#( $n$ [, $a$ ]) 1 ≤ $a$ ≤ 9、1 ≤ $a$ ≤ 999（ $a$ 、 $n$ は整数）

$n$ ：試行回数を表します。一度に発生させる乱数の個数を指定します。

$a$ ： Ran#と同様です。

例: （Ran# 0を実行直後）RanList#(3,1) = {0.701320948,0.9297706456,0.2939058016}

Random Sample from List RanSamp#(,)

リストからランダムに要素を取り出して、結果をリスト形式で返します。

構文： RanSamp#(List, $n$ [, $m$ ])

List：リスト変数（List 1～List 26またはList Ans）^*、またはリスト

リスト変数は、サブネームで指定することもできます。

$n$ ：試行回数（ $m$ = 0 のとき1 ≤ $n$ ≤ 999、 $m$ = 1のとき1 ≤ $n$ ≤ リストの要素数）

$m$ ： 0または1を指定します（省略時は0）。 $m$ = 0のとき、各要素を複数回抽出できます。 $m$ ＝1のとき、各要素を抽出できるのは1回だけです。

例: {1,3,6,7}から、要素をランダムに2個取り出す： RanSamp#({1,3,6,7},2,1)
{1,3,6,7}から、要素をランダムに5回取り出す： RanSamp#({1,3,6,7},5)

Numeric Calc（数値計算）

GCD GCD(,)

複数の整数の最大公約数を求めます。

構文：　GCD( $n$ , $m$ )

LCM LCM(,)

複数の整数の最小公倍数を求めます。

構文：　LCM( $n$ , $m$ )

Absolute Value Abs()

引数 $n$ の絶対値を求めます。

構文： | $n$ | Abs( $n$ )

Integer Part Int()

引数 $n$ の整数部分を抽出します。

構文： Int( $n$ )

例: Int(-3.5) = -3

Fraction Part Frac()

引数 $n$ の小数部分を抽出します。

構文： Frac( $n$ )

例: Frac(-3.5) = -0.5

Round Off Rnd

CalculateアプリのCalculationタブで使用可能な関数です。直前の計算結果（Ans）の数値を、S > [Display]の設定に従った結果表示のとおりに丸めます。

構文： Rnd　（引数なし、直前の計算結果に対してのみ有効）

例: [Display] > [Fix3: 0.123]のとき、10÷3を計算し、続いてAns×3を計算する

Rndを使わなかった場合

10*3E
/3E

Rndを使った場合

10*3E
C > [Numeric Calc] > [Round Off]E
/3E

[Display] > [Fix3: 0.123]のとき10÷3=3.333と表示されますが、内部数値は15桁を保持しているため、Ans×3=10.000となります。Rndを使って10÷3の計算結果を表示どおりに丸めると、Ans×3=9.999となります。

Largest Integer Intg()

引数 $n$ を超えない最大の整数値を返します。

構文： Intg( $n$ )

例: Intg(-10.56) = -11

Round Internal RndFix()

引数 $n$ を、指定した小数点以下桁数 $m$ （0～9）の次の桁で四捨五入して丸めます。

構文： RndFix( $n$ [, $m$ ])

$m$ を省略するとRnd関数と同様に、S > [Display]の設定に従って丸めます。

構文内では使用不可： $d / d x$ 、 $d^{2} / d x^{2}$ 、 $∫ d x$ 、Σ、FMin、FMax、Solve、RndFix、logab

例: RndFix(1.23456,3) = 1.235

Division Remainder MOD(,)

除算の余りを求める関数です。 $n$ を $m$ で割ったときの余りを返します。

構文： MOD( $n$ , $m$ ) ( $n$ 、 $m$ は整数）

例: MOD(17,3) = 2

Remainder Exponentiation MOD_Exp(,,)

べき剰余を求める関数です。 $n$ を $p$ 乗した値を $m$ で割ったときの余りを返します。

構文： MOD_Exp( $n$ , $p$ , $m$ ) ( $n$ 、 $p$ 、 $m$ は整数）

例: MOD(2,4,3) = 1

Vector（ベクトル計算）

構文中のVct $n$ 、Vct $m$ は、ベクトルまたはベクトル変数です。

例に記載されているベクトル（“ $[\begin{matrix} 1 & 2 \end{matrix}]$ ”など）は、T > [m×n]を使って入力します。詳しくは、計算式の中にベクトルを入力するを参照してください。

参考

内積、外積、ベクトルのなす角を計算する場合は、2つのベクトルの次元が同じでなければなりません。

Vector Vct

“Vct ”を入力します。続けてA～ZまたはAnsを入力することで、ベクトル変数を指定します。

Dot Product DotP(,)

2つのベクトルの内積を求めます。

構文： DotP(Vct $n$ ,Vct $m$ )

例: DotP( $[\begin{matrix} 1 & 2 \end{matrix}]$ , $[\begin{matrix} 3 & 4 \end{matrix}]$ ) = 11

Cross Product CrossP(,)

2つのベクトルの外積を求めます。

構文： CrossP(Vct $n$ ,Vct $m$ )　（Vct $n$ 、Vct $m$ の次元は1×2、1×3、2×1、または3×1であること）

例: CrossP( $[\begin{matrix} 1 & 2 \end{matrix}]$ , $[\begin{matrix} 3 & 4 \end{matrix}]$ ) = $[\begin{matrix} 0 & 0 & - 2 \end{matrix}]$

‎2-Vector Angle Angle(,)

2つのベクトルのなす角を求めます。

構文： Angle(Vct $n$ ,Vct $m$ )

例: S > [Angle] > [Radian]のとき、Angle( $[\begin{matrix} 1 & 1 \end{matrix}]$ , $[\begin{matrix} - 1 & 1 \end{matrix}]$ ) = $\frac{1}{2} π$

Unit Vector UnitV()

引数に指定したベクトルの単位ベクトルを求めます。

構文： UnitV(Vct $n$ )

例: UnitV( $[\begin{matrix} 5 & 5 \end{matrix}]$ ) = $[\begin{matrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{matrix}]$

Vector Norm Norm()

引数に指定したベクトルまたは行列のノルム（大きさ）を求めます。

構文： Norm(Vct $n$ ) ; Norm(Mat $n$ )　（Mat $n$ は行列または行列変数）

例: Norm( $[\begin{matrix} 1 & 3 \end{matrix}]$ ) = $\sqrt{10}$ ; Norm( $[\begin{matrix} 1 & 3 \\ 2 & 4 \end{matrix}]$ ) = $\sqrt{30}$

Matrix（行列計算）

構文中のMat $n$ 、Mat $m$ は、行列または行列変数です。

例に記載されている行列（“ $[\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix}]$ ”など）は、T > [m×n]を使って入力します。詳しくは、計算式の中に行列を入力するを参照してください。

参考

行列式および逆行列は、桁落ちにより誤差が生じることがあります。

階段形の行列および被約階段形の行列は、桁落ちにより精度が出ない場合があります。

Matrix Mat

“Mat ”を入力します。続けてA～ZまたはAnsを入力することで、行列変数を指定します。

Inverse Matrix ^-1

指定した正方行列の逆行列を求めます。

構文： Mat $n^{- 1}$

例: ${[\begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix}]}^{- 1}$ = $[\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}]$

注意事項

行列式が0に近い行列を使って計算を行うと、精度が出ない場合があります。

Determinant Det()

指定した正方行列の行列式を求めます。

構文： Det(Mat $n$ )

例: Det( $[\begin{matrix} 1 & 3 \\ 2 & 4 \end{matrix}]$ ) = -2

Matrix Transpose Trn()

指定した行列の転置行列を求めます。

構文： Trn(Mat $n$ )

例: Trn( $[\begin{matrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{matrix}]$ ) = $[\begin{matrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{matrix}]$

参考

“Trn”コマンドは、ベクトルにも使うことができます。1行× $n$ 列のベクトルを $n$ 行×1列のベクトルに変換、または $m$ 行×1列のベクトルを1行× $m$ 列のベクトルに変換します。

Matrix Identity Identity()

指定した行数・列数の単位行列を作成します。

構文： Identity( $n$ ) （ $n$ は整数)

例: Identity(2) = $[\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}]$

Row Echelon Form Ref()

ガウスの消去法アルゴリズムを用いて、指定した行列の階段形の行列（Row Echelon Form）を求めます。

構文： Ref(Mat $n$ )

例: Ref( $[\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix}]$ ) = $[\begin{matrix} 1 & \frac{5}{4} & \frac{3}{2} \\ 0 & 1 & 2 \end{matrix}]$

Reduced Row Echelon Form Rref()

指定した行列の被約階段形の行列（Reduced Row Echelon Form）を求めます。

構文： Rref(Mat $n$ )

例: Rref( $[\begin{matrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{matrix}]$ ) = $[\begin{matrix} 1 & 0 & - 1 \\ 0 & 1 & 2 \end{matrix}]$

Matrix Augment Augment(,)

行数が等しい2つの行列（またはベクトル）を、1つの行列に結合します。

構文： Augment(Mat $m$ ,Mat $n$ ) ; Augment(Vct $m$ ,Vct $n$ )

構文中のMat $m$ とMat $n$ の片方または両方をVct $m$ 、Vct $n$ に置き換え可能です。

例: Augment( $[\begin{matrix} 1 & 3 \\ 2 & 4 \end{matrix}]$ , $[\begin{matrix} 2 & 6 \\ 4 & 8 \end{matrix}]$ ) = $[\begin{matrix} 1 & 3 & 2 & 6 \\ 2 & 4 & 4 & 8 \end{matrix}]$ ; Augment( $[\begin{matrix} 1 \\ 2 \end{matrix}]$ , $[\begin{matrix} 2 & 6 \\ 4 & 8 \end{matrix}]$ ) = $[\begin{matrix} 1 & 2 & 6 \\ 2 & 4 & 8 \end{matrix}]$

Fill Matrix Fill(,)

行列変数内（またはベクトル変数内）のすべての要素を、指定した同じ値 $m$ に置き換えます。

構文： Fill( $m$ ,Mat $n$ ) ; Fill( $m$ ,Vct $n$ )

Dimensions Dim()

行列（またはベクトル）の次元を取得し、リスト形式で出力します。

構文1： Dim(Mat $n$ ) ; Dim(Vct $n$ )

“Dim”コマンドの結果はリストなので、List Ansに保存されます。

次元をリスト形式で指定して、すべての要素が0の行列（またはベクトル）を作成します。

構文2： { $a$ , $b$ } → Dim(Mat $n$ )　( $a$ 、 $b$ は整数、1 ≤ $a$ ≤ 999、1 ≤ $b$ ≤ 999) ;

{ $a$ , $b$ } → Dim(Vct $n$ )　( $a$ 、 $b$ は整数、 $a$ = 1のとき1 ≤ $b$ ≤ 999、 $b$ = 1のとき1 ≤ $a$ ≤ 999)

Complex Number（複素数計算）

構文中の“ $z$ ”は複素数を表します。Arg、Ir∠θ、Ia+b $i$ を使った計算はS > [Angle]に影響されます。

参考

本機はa+b $i$ の形で表される複素数をガウス平面上の座標と見なし、絶対値| $z$ |と偏角Arg( $z$ )を計算します。

Norm of a Complex Number Abs()

複素数の絶対値を求めます。

構文： | $z$ | Abs( $z$ )

例: |1+ $i$ | = $\sqrt{2}$

Argument Arg()

複素数の偏角を求めます。

構文： Arg( $z$ )

例: Arg(1+ $i$ ) = $\frac{1}{4} π$ (S > [Angle] > [Radian])

Complex Conjugate Conjg()

共役複素数を求めます。

構文： Conjg( $z$ )

例: Conjg(1+ $i$ ) = 1 $- i$

Real Part ReP()

複素数の実部を抽出します。

構文： ReP( $z$ )

例: ReP(1+2 $i$ ) = 1

Imaginary Part ImP()

複素数の虚部を抽出します。

構文： ImP( $z$ )

例: ImP(1+2 $i$ ) = 2

Ir∠θ Ir∠θ

直交形式の値を極形式に変換します。

構文： $z$ Ir∠θ

例: $1 + \sqrt{3} i$ Ir∠θ = 2∠ $\frac{1}{3} π$ (S > [Angle] > [Radian])

Ia+b $i$ Ia+b $i$

極形式の値を直交形式に変換します。

構文： $z$ Ia+b $i$

例: 2∠ $\frac{1}{3} π$ Ia+b $i$ = $1 + \sqrt{3} i$ (S > [Angle] > [Radian])

Statistics（統計計算）

構文中の“List $n$ ”、“List $m$ ”は、リストまたはリスト変数です。リスト変数の場合、 $n$ 、 $m$ は1～26またはAnsです。リスト変数は、サブネームで指定することもできます。

{} {}

リストを入力するための { } を入力します。

List List

“List ”を入力します。続けて1～26またはAnsを入力することで、リスト変数を指定します。

Dimensions Dim()

リスト内の要素数を求めます。

構文1： Dim(List $n$ )

リストの要素数を指定して、すべての要素が0のリスト変数を作成します。

構文2：要素数 $a$ → Dim(List $n$ )　(1 ≤ $a$ ≤ 999、 $a$ は整数)

Fill List Fill(,)

リスト変数内のすべての要素を、指定した同じ値 $a$ に置き換えます。

構文： Fill( $a$ ,List $n$ )

Generate Sequence Seq(,,,,)

functionを定義して数列を生成し、リスト形式で返します。

構文： Seq( $f (x)$ , $x$ ,開始値,終了値,ステップ値)

$x$ には任意のアルファ変数を指定できます。

例: Seq( $x^{2}$ , $x$ ,1,11,5) = {1,36,121}

Minimum Min()

構文1： Min(List $n$ )　リストの全要素の中から最小値を抽出します。

構文2： Min(List $n$ ,List $m$ )　2つのリストの同じ位置の要素からより小さい方を抽出します。

Maximum Max()

構文1： Max(List $n$ )　リストの全要素の中から最大値を抽出します。

構文2： Max(List $n$ ,List $m$ )　2つのリストの同じ位置の要素からより大きい方を抽出します。

Mean Mean()

リストに含まれる全要素の平均値を求めます。

構文： Mean(List $n$ )

Median Median()

2つのリストの片方をデータ、もう片方を度数とみなし、そのデータの中央値を求めます。

構文： Median(List $n$ ,List $m$ )

List $n$ ：データリスト、List $m$ ：度数リスト。List $n$ 、List $m$ の要素数は同一であること。

例: Lst 1 = {36,16,58,46,56}、List 2 = {75,89,98,72,67}のとき、Median(List 1,List 2) = 46

Combine Lists Augment(,)

2つのリストを1つに結合します。

構文： Augment(List $n$ ,List $m$ )

Sum of List Elements Sum()

リストに含まれる全要素の総和を求めます。

構文： Sum(List $n$ )

List Product Prod()

リストに含まれる全要素の総積を求めます。

構文： Prod(List $n$ )

Cumulative Frequency Cuml()

リストの各要素の累積度数を計算します。

構文： Cuml(List $n$ )

例: 例： List 1 = {2,3,6,5,4}のとき、Cuml(List 1) = {2,5,11,16,20}

Data Percentages Percent()

リストの全要素の総和に対する、各要素のパーセンテージを計算します。

構文： Percent(List $n$ )

List Data Diff ΔList

要素数 $n$ ( $n$ ≥ 2)のリストにおいて、{要素2 − 要素1, 要素3 − 要素2, … 要素 $n$ − 要素 $n$ −1} を計算し、結果をリスト形式で返します。

構文： ∆List $a$ 　（ $a$ はリスト変数の番号）

補足： “∆List 1→List 2”と入力することで、計算結果をList 2に保存できます。

Estimated x-Data $\hat{x}$
Estimated y-Data $\hat{y}$

これらの関数は、Statisticsアプリで回帰計算を実行した直後^*に使います。一方の変数（ $x$ または $y$ ）の値を指定し、回帰モデルに基づく他方の変数の推定値を求めます。

構文： $y$ 値 $\hat{x}$ 　（ $y$ 値に対する $x$ の推定値を計算）

$x$ 値 $\hat{y}$ 　（ $x$ 値に対する $y$ の推定値を計算）

下記タイプの回帰モデルについては、推定値を求めることはできません。
Med-Med Regression、Quadratic Regression、Cubic Regression、Quartic Regression、Sinusoidal Regression、Logistic Regression

Sample Standard Deviation StdDev()

リストで指定したデータの標本標準偏差を求めます。

構文： StdDev(List $n$ [,List $m$ ])　（List $n$ ... 標本データ、List $m$ ... 度数データ）

例: StdDev({10,20,30,40},{3,5,4,1}) = 9.26808696

Population Standard Deviation StdDev_σ()

リストで指定したデータの母標準偏差を求めます。

構文： StdDev_σ(List $n$ [,List $m$ ])　（List $n$ ... 標本データ、List $m$ ... 度数データ）

Unbiased Variance Variance()

リストで指定したデータの不偏分散を求めます。

構文： Variance(List $n$ [,List $m$ ])　（List $n$ ... 標本データ、List $m$ ... 度数データ）

Population Variance Variance_ $σ^{2}$ ()

リストで指定したデータの母分散を求めます。

構文： Variance_ $σ^{2}$ (List $n$ [,List $m$ ])　（List $n$ ... 標本データ、List $m$ ... 度数データ）

List to Matrix List→Mat()

リストの内容を、Mat Ansに保存します。

構文： List→Mat(List $n$ ,List $m$ )　（List $n$ 、List $m$ の要素数は同一であること。）

例: List 1 = {2,3,4}、List 2 = {20,30,40}のとき、List→Mat(List 1,List 2) = $[\begin{matrix} 2 & 20 \\ 3 & 30 \\ 4 & 40 \end{matrix}]$

Matrix to List Mat→List()

行列変数の指定列を、List Ansに保存します。

構文： Mat→List(Mat $n$ , $m$ )　（ $n$ はA～ZまたはAns、 $m$ は列番号）

例: Mat A = $[\begin{matrix} 2 & 20 \\ 3 & 30 \\ 4 & 40 \end{matrix}]$ のとき、Mat→List(Mat A,1) = {2,3,4}

補足： “Mat→List(Mat A,1)→List 1”と入力することで、Mat Aの1列目の要素をList 1に代入できます。

Distribution（分布）: 標準正規分布の確率値計算

本節で説明する各関数は、Statisticsアプリで1変数統計計算を実行した直後に使います。

Normal Probability P(t)     P()
Normal Probability‎ Q(t)     Q()
Normal Probability R(t)     R()

標準化変量 $t$ を引数に取り、標準正規分布の下図に示す確率値を求めます。 $t$ の値は、関数t()を使って求めます。

構文： P( $t$ ) ; Q( $t$ ) ; R( $t$ )

Normal Variable t(x) t()

データ値 $x$ における標準化変量t( $x$ )を、1変数統計計算の結果として得られた平均値 $\bar{x}$ と母標準偏差 $σ_{x}$ に基づいて、次の式により求めます。

$t (x) = \frac{x - \bar{x}}{σ_{x}}$

構文： t( $x$ )

この関数はP()、Q()、R()と組み合わせて、標準正規分布の確率値を求めるのに使います。

例: ある大学の学生20人の身長データをStatisticsアプリに入力し、1変数統計計算を実行した。この20人の中で身長180cmのA君が、上位から何%に入るかを求める。

R(t(180))

Distribution（分布）: 各種分布計算

本節で説明する各関数は、それぞれ異なる分布計算を実行します。

構文に関する留意点

構文中の文字・用語の意味は下記のとおりです。

$x$ : データ値

Lower: 下界

Upper: 上界

$μ$ ：母平均

$σ$ ：母標準偏差（ $σ$ > 0）

$λ$ ：平均（ $λ$ > 0）

$p$ : 確率（0 ≤ $p$ ≤ 1）

df: 自由度（df > 0）

$n$ :df: 自由度の分子（正の整数）

$d$ :df: 自由度の分母（正の整数）

$P$ : 成功確率（0 ≤ $P$ ≤ 1）

$n$ : 母集団からの試行回数（0 ≤ $n$ の整数）

$M$ : 母集団における成功数（0 ≤ $M$ の整数）

$N$ : 母集団の大きさ（ $n$ ≤ $N$ 、 $M$ ≤ $N$ の整数）

カッコ（[ ]）で囲まれた引数の入力を省略した場合は、下記の値が使われます。
$μ$ =0、 $σ$ =1、tail=“L” (Left)

計算結果が格納される変数について

各関数による計算結果が格納される変数（p、xInv、x1InvN、x2InvN、zLow、zUp、tLow、tUp）は、C > [Variable Data] > [Distribution]から呼び出すことができます。

Normal Probability Density NormPD()

指定したデータに対する正規確率密度（ $p$ 値）を返します。

構文： NormPD( $x$ [, $μ$ , $σ$ ])

$x$ には単一の数値またはリストを指定できます。計算結果は、変数 $p$ およびAns（ $x$ がリストの場合はList Ans）に格納されます。

例: NormPD(1) = 0.2419707245 ; NormPD({0.5,1}) = {0.3520653268,0.2419707245}

Normal Cumulative Dist NormCD(,)

指定したデータに対する正規累積確率（ $p$ 値）を返します。

構文： NormCD(Lower,Upper[, $μ$ , $σ$ ])

Lower、Upperにはそれぞれ単一の数値またはリストを指定できます。計算結果 $p$ 、zLow、zUpの各値は、変数 $p$ 、zLow、zUpにそれぞれ格納されます。また計算結果はAns（Lower、Upperがリストの場合はList Ans）にも格納されます。

例: NormCD(-1,1) = 0.6826894921 ; NormCD({-1,-2},{1,2}) = {0.6826894921,0.9544997361}

Inverse Normal Cumul Dist InvNormCD()

指定した $p$ 値に基づいて、正規累積分布逆演算した値（Lower値かUpper値の片方、または両方）を返します。

構文： InvNormCD([tail,] $p$ [, $μ$ , $σ$ ])

“tail”にはLeft、Right、またはCenterのいずれかを指定します。指定するには、下記の数値または文字を入力します。

Left： -1または“L”

Center： 0または“C”

Right： 1または“R”

$p$ には単一の数値またはリストを指定できます。計算結果は“tail”の設定に応じて次のように出力されます。

tail = Left時	Upper値が変数x1InvNおよびAns（ $p$ がリストの場合はList Ans）に格納されます。
tail = Right時	Lower値が変数x1InvNおよびAns（ $p$ がリストの場合はList Ans）に格納されます。
tail = Central時	Lower、Upper値がそれぞれ変数x1InvN、x2InvNに格納されます。Lower値のみAns（ $p$ がリストの場合はList Ans）にも格納されます。

例: InvNormCD(“L”,0.7,35,2) = 36.04880103
InvNormCD({0.5,0.7},35,2) = {35,36.04880103}

t Probability Density tPD(,)

指定したデータに対するスチューデントの $t$ 確率密度（ $p$ 値）を返します。

構文： tPD( $x$ ,df)

解説は確率の構文を参照

例: tPD(1,1) = 0.1591549431 ; tPD({0,1},1) = {0.3183098862,0.1591549431}

t Cumulative Distribution tCD(,,)

指定したデータに対するスチューデントの $t$ 累積確率（ $p$ 値）を返します。

構文： tCD(Lower,Upper,df)

Lower、Upperにはそれぞれ単一の数値またはリストを指定できます。計算結果 $p$ 、tLow、tUpの各値は、変数 $p$ 、tLow、tUpにそれぞれ格納されます。また計算結果はAns（Lower、Upperがリストの場合はList Ans）にも格納されます。

例: tCD(0,1,1) = 0.25 ; tCD({0,0},{1,2},1) = {0.25,0.3524163823}

Inverse t Cumulative Dist InvTCD(,)

指定した $p$ 値に基づいて、スチューデントの $t$ 累積分布逆演算したLower値を返します。

構文： InvTCD( $p$ ,df)

解説は連続型分布逆演算の構文を参照

例: InvTCD(0.25,1) = 1 ; InvTCD({0.25,0.75},1) = {1,-1}

‎ $χ^{2}$ ‎ Probability Density ChiPD(,)

指定したデータに対する $χ^{2}$ 確率密度（ $p$ 値）を返します。

構文： ChiPD( $x$ ,df)

解説は確率の構文を参照

例: ChiPD(1,1) = 0.2419707245 ; ChiPD({0,1},1) = {0,0.2419707245}

‎ $χ^{2}$ ‎ Cumulative Distribution ChiCD(,,)

指定したデータに対する $χ^{2}$ 累積確率（ $p$ 値）を返します。

構文： ChiCD(Lower,Upper,df)

解説は累積確率の構文を参照

例: ChiCD(0,1,1) = 0.6826894921 ; ChiCD({0,0},{1,2},1) = {0.6826894921,0.8427007929}

Inverse‎ ‎ $χ^{2}$ Cumulative Dist InvChiCD(,)

指定した $p$ 値に基づいて、 $χ^{2}$ 累積分布逆演算したLower値を返します。

構文： InvChiCD( $p$ ,df)

解説は連続型分布逆演算の構文を参照

例: InvChiCD(0.319,1) = 0.9930420738 ; InvChiCD({0.64,0.319},1) = {0.2187421667,0.9930420738}

F Probability Density FPD(,,)

指定したデータに対する $F$ 確率密度（ $p$ 値）を返します。

構文：FPD( $x$ , $n$ :df, $d$ :df)

解説は確率の構文を参照

例: FPD(1,1,2) = 0.1924500897 ; FPD({1,2},1,2) = {0.1924500897,0.08838834765}

F Cumulative Distribution FCD(,,,)

指定したデータに対する $F$ 累積確率（ $p$ 値）を返します。

構文：FCD(Lower,Upper, $n$ :df, $d$ :df)

解説は累積確率の構文を参照

例: FCD(0,1,1,2) = 0.5773502692 ; FCD({0,0},{1,2},1,2) = {0.5773502692,0.7071067812}

Inverse F Cumulative Dist InvFCD(,,)

指定した $p$ 値に基づいて、 $F$ 累積分布逆演算したLower値を返します。

構文：InvFCD( $p$ , $n$ :df, $d$ :df)

解説は連続型分布逆演算の構文を参照

例: InvFCD(0.43,1,2) = 0.9625240705 ; InvFCD({0.86,0.43},1,2) = {0.03998368013,0.9625240705}

Binomial Probability BinomialPD(,)

指定したデータに対する2項確率（ $p$ 値）を返します。

構文： BinomialPD([ $x$ ,] $n$ , $P$ )

解説は確率の構文を参照

例: BinomialPD(3,5,0.5) = 0.3125 ; BinomialPD({3,5},5,0.5) = {0.3125,0.03125}

Binomial Cumulative Dist BinomialCD(,)

指定したデータに対する2項累積確率（ $p$ 値）を返します。

構文： BinomialCD([[Lower,]Upper,] $n$ , $P$ )

解説は累積確率の構文を参照

例: BinomialCD(5,10,0.5) = 0.623046875 ; BinomialCD({0,5},{5,8},10,0.5) = {0.623046875,0.6123046875}

Inverse Binomial Cumulative Dist InvBinomialCD(,,)

指定した $p$ 値に基づいて、2項累積分布逆演算した値を返します。

構文： InvBinomialCD( $p$ , $n$ , $P$ )

解説は離散型分布逆演算の構文を参照

例: InvBinomialCD(0.6,10,0.5) = 5 ; InvBinomialCD({0.6,0.3},10,0.5) = {5,4}

注意事項

本機は指定された $p$ 値と、その $p$ 値から最小有効桁で1を引いた数値（ $p$ ’値）の2つの値を使って計算します。 $p$ 値で計算した結果は変数xInvに格納され、 $p$ ’値で計算した結果は変数*xInvに格納されます。本機は常にxInvのみを計算結果として表示します。ただし、xInvと*xInvの値が異なる場合は警告メッセージが現れ、両方の値が表示されます。

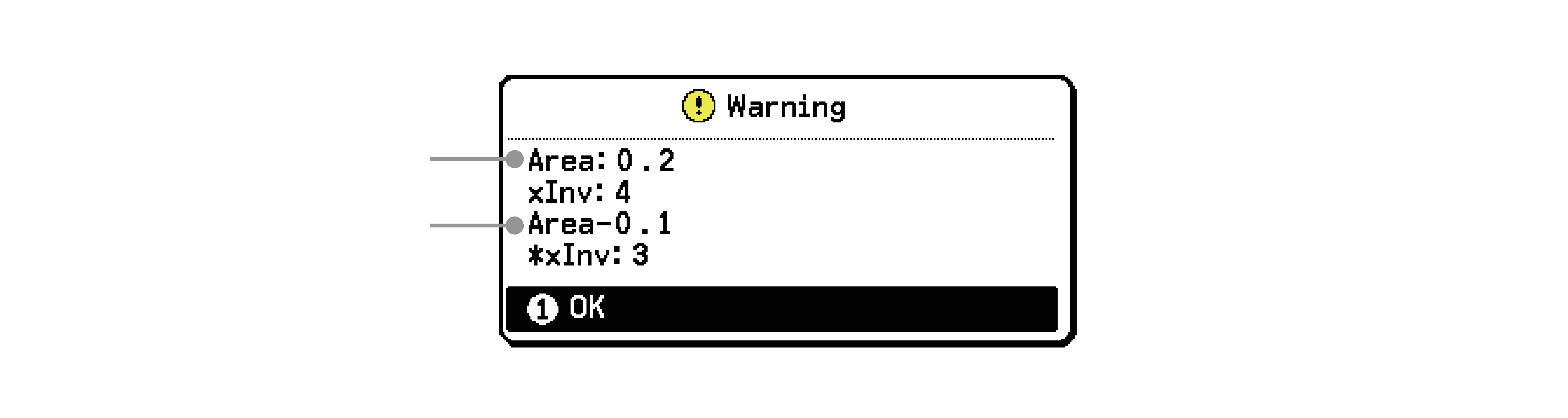
CY875_V2_Catalog Distribution_2 + CY875_V2_Catalog Distribution_2

$p$ 値

$p$ ’値

計算結果（xInvと＊xInvの値）は、整数となります。 $p$ 値が10桁以上の場合、精度が落ちます。計算精度のわずかな差が計算結果に影響する点にご注意ください。

Poisson Probability PoissonPD(,)

指定したデータに対するポアソン確率（ $p$ 値）を返します。

構文： PoissonPD( $x$ , $λ$ )

解説は確率の構文を参照

例: PoissonPD(1,1.2) = 0.3614330543 ; PoissonPD({1,2},1.2) = {0.3614330543,0.2168598326}

Poisson Cumulative Dist PoissonCD(,)

指定したデータに対するポアソン累積確率（ $p$ 値）を返します。

構文： PoissonCD([Lower,]Upper, $λ$ )

解説は累積確率の構文を参照

Lowerを省略するとLower = 0とみなされます。

例: PoissonCD(1,2,1.2) = 0.5782928869 ; PoissonCD({1,1},{2,3},1.2) = {0.5782928869,0.6650368199}

Inverse Poisson Cumul Dist InvPoissonCD(,)

指定した $p$ 値に基づいて、ポアソン累積分布逆演算した値を返します。

構文： InvPoissonCD( $p$ , $λ$ )

解説は離散型分布逆演算の構文を参照

例: InvPoissonCD(0.58,1.2) = 1 ; InvPoissonCD({0.58,0.75},1.2) = {1,2}

注意事項は、Inverse Binomial Cumulative Distと同様です。

Geometric Probability GeoPD(,)

指定したデータに対する幾何確率（ $p$ 値）を返します。

構文： GeoPD( $x$ , $P$ )

解説は確率の構文を参照

例: GeoPD(2,0.8) = 0.16 ; GeoPD({2,3},0.8) = {0.16,0.032}

Geometric Cumulative Dist GeoCD(,)

指定したデータに対する幾何累積確率（ $p$ 値）を返します。

構文： GeoCD([Lower,]Upper, $P$ )

解説は累積確率の構文を参照

Lowerを省略するとLower = 0とみなされます。

例: GeoCD(1,2,0.8) = 0.96 ; GeoCD({1,1},{2,3},0.8) = {0.96,0.992}

Inverse Geometric Cumul Dist InvGeoCD(,)

指定した $p$ 値に基づいて、幾何累積分布逆演算した値を返します。

構文： InvGeoCD( $p$ , $P$ )

解説は離散型分布逆演算の構文を参照

例: InvGeoCD(0.96,0.8) = 2 ; InvGeoCD({0.96,0.992},0.8) = {2,3}

注意事項は、Inverse Binomial Cumulative Distと同様です。

Hypergeometric Probability HypergeoPD(,,,)

指定したデータに対する超幾何確率（ $p$ 値）を返します。

構文： HypergeoPD( $x$ , $n$ , $M$ , $N$ )

解説は確率の構文を参照

例: HypergeoPD(1,5,10,20) = 0.1354489164 ; HypergeoPD({1,2},5,10,20) = {0.1354489164,0.3482972136}

Hypergeometric Cumul Dist HypergeoCD(,,,)

指定したデータに対する超幾何累積確率（ $p$ 値）を返します。

構文： HypergeoCD([Lower,]Upper, $n$ , $M$ , $N$ )

解説は累積確率の構文を参照

Lowerを省略するとLower = 0とみなされます。

例: HypergeoCD(1,2,5,10,20) = 0.48374613 ; HypergeoCD({1,1},{2,3},5,10,20) = {0.48374613,0.8320433437}

Inverse Hypergeo Cumul Dist InvHypergeoCD(,,,)

指定した $p$ 値に基づいて、超幾何累積分布逆演算した値を返します。

構文： InvHypergeoCD( $p$ , $n$ , $M$ , $N$ )

解説は離散型分布逆演算の構文を参照

例: InvHypergeoCD(0.48,5,10,20) = 2 ; InvHypergeoCD({0.48,0.83},5,10,20) = {2,3}

注意事項は、Inverse Binomial Cumulative Distと同様です。

構文と解説

構文	解説
確率の構文	$x$ には単一の数値またはリストを指定できます。計算結果は、変数 $p$ およびAns（ $x$ がリストの場合はList Ans）に格納されます。
累積確率の構文	Lower、Upperにはそれぞれ単一の数値またはリストを指定できます。計算結果は、変数 $p$ およびAns（Lower、Upperがリストの場合はList Ans）に格納されます。
連続型分布逆演算の構文	$p$ には単一の数値またはリストを指定できます。計算結果のLower値は、変数xInvおよびAns（ $p$ がリストの場合はList Ans）に格納されます。
離散型分布逆演算の構文	$p$ には単一の数値またはリストを指定できます。計算結果のX値は、変数xInvおよびAns（ $p$ がリストの場合はList Ans）に格納されます。

Angle/Coord/Sexa（角度/座標/度分秒）

Degrees °

数値の角度単位を度数法に指定します。

構文： $n$ °

例: S > [Angle] > [Radian]のとき、90° = $\frac{1}{2} π$

Radians $^{r}$

数値の角度単位を弧度法に指定します。

構文： $n^{r}$

例: S > [Angle] > [Degree]のとき、 $\frac{π}{2}^{r}$ = 90

Gradians $^{g}$

数値の角度単位をグラジアンに指定します。

構文： $n^{g}$

例: S > [Angle] > [Degree]のとき、 $100^{g}$ = 90

Rectangular to Polar Pol(,)

数値を直交座標から極座標に変換し、リスト形式で返します。

構文： Pol( $x$ , $y$ ) = ( $r$ , $θ$ )

極座標の計算結果の $θ$ は、S > [Angle]の設定に応じて下記の範囲で表示されます。

“Degree”（度数法）の場合: -180 < $θ$ ≤ 180

“Radian”（弧度法）の場合: - $π$ < $θ$ ≤ $π$

“Gradian”（グラジアン）の場合: -200 < $θ$ ≤ 200

例: S > [Angle] > [Radian]のとき、Pol( $\sqrt{2}$ , $\sqrt{2}$ ) = {2, $\frac{1}{4} π$ }

Polar to Rectangular Rec(,)

数値を極座標から直交座標に変換し、リスト形式で返します。

構文： Rec( $r$ , $θ$ ) = ( $x$ , $y$ )

例: S > [Angle] > [Radian]のとき、Rec(2, $\frac{1}{4} π$ ) = { $\sqrt{2}$ , $\sqrt{2}$ }

Degs Mins Secs °

数値を60進数で入力します。

構文：度の数値°[分の数値°[秒の数値°]]

例: 1°15° = 1.25 ; 0°75° = 1.25 ; 0°15° = 0.25 ; 0°0°900° = 0.25

補足：計算結果を60進数で表示するには、sF > [Sexagesimal]を選びます。詳しくは、計算結果の表示変換（Formatメニュー）を参照してください。

Decimal to Sexagesimal IDMS

10進数を60進数（度分秒の数値）に変換します。

構文： $n$ IDMS

例: 1.25IDMS = 1°15’00”

Hyperbolic Calc（双曲線関数・逆双曲線関数）

下記の双曲線関数と逆双曲線関数を入力します。

メニュー項目	関数
sinh	sinh()
cosh	cosh()
tanh	tanh()
sinh‎ $^{-1}$ ‎	sinh $^{-1}$ ()
cosh‎ $^{-1}$ ‎	cosh $^{-1}$ ()
tanh‎ $^{-1}$ ‎	tanh $^{-1}$ ()

例: sinh(1) = 1.175201194 ; sinh $^{-1}$ (Ans) = 1

Engineer Symbol（エンジニアリング記号）

下記のエンジニアリング記号を入力します。

メニュー項目	記号	$10^{n}$
Milli	m	$10^{-3}$
Micro	μ	$10^{-6}$
Nano	n	$10^{-9}$
Pico	p	$10^{-12}$
Femto	f	$10^{-15}$
Kilo	k	$10^{3}$
Mega	M	$10^{6}$
Giga	G	$10^{9}$
Tera	T	$10^{12}$
Peta	P	$10^{15}$
Exa	E	$10^{18}$

エンジニアリング記号を数値の直後に付記すると、記号に応じて数値が $10^{n}$ 倍されます（ $n$ は3の整数倍）。

例: 7.1k = 7100 ; 2G÷100M = 20

補足：計算結果をエンジニアリング記号付きで表示するには、S > [Display] > [Engineer Symbol]をオンにします。詳しくは、Display（一般）を参照してください。

Unit Conversions（単位換算）

ある単位の数値を、異なる単位の数値に変換します。

構文： $n$ 単位コマンド Unit Conversions 単位コマンド　（ $n$ は実数、または実数のリスト）

2つの単位コマンドを“ Unit Conversions ”でつなぎ、1つの単位換算コマンドとして使います。2つの単位コマンドは、必ず同じカテゴリーのものから選びます。使用できる単位コマンドは、下記の「単位コマンド一覧」を参照してください。

例: 25.4 [cm] Unit Conversions [in] = 10 ; {175,162} [m²] [ha] = {0.0175,0.0162}

単位コマンド一覧

カテゴリー	単位コマンド
Length	[fm]
	[Å]
	[μm]
	[mm]
	[cm]
	[m]
	[km]
	[AU]
	[l.y.]
	[pc]
	[Mil]
	[in]
	[ft]
	[yd]
	[fath]
	[rd]
	[mile]
	[n mile]
Area	[cm²]
	[m²]
	[ha]
	[km²]
	[in²]
	[ft²]
	[yd²]
	[acre]
	[mile²]
Volume	[cm³]
	[mL]
	[L]
	[m³]
	[in³]
	[ft³]
	[fl_oz(UK)]
	[fl_oz(US)]
	[gal(US)]
	[gal(UK)]
	[pt]
	[qt]
	[tsp]
	[tbsp]
	[cup]
Time	[ns]
	[μs]
	[ms]
	[s]
	[min]
	[h]
	[day]
	[week]
	[yr]
	[s-yr]
	[t-yr]
Temperature	[°C]
	[K]
	[°F]
	[°R]
Velocity	[m/s]
	[km/h]
	[knot]
	[ft/s]
	[mile/h]
Mass	[u]
	[mg]
	[g]
	[kg]
	[mton]
	[oz]
	[lb]
	[slug]
	[ton(short)]
	[ton(long)]
Force	[N]
	[lbf]
	[tonf]
	[dyne]
	[kgf]
Pressure	[Pa]
	[kPa]
	[mmH₂O]
	[mmHg]
	[atm]
	[inH₂O]
	[inHg]
	[lbf/in²]
	[bar]
	[kgf/cm²]
Energy	[eV]
	[J]
	[cal_th]
	[cal₁₅]
	[cal_IT]
	[kcal_th]
	[kcal₁₅]
	[kcal_IT]
	[l-atm]
	[kW･h]
	[ft･lbf]
	[Btu]
	[erg]
	[kgf･m]
Power	[W]
	[cal_th/s]
	[hp]
	[ft･lbf/s]
	[Btu/min]

Variable Data（アプリデータ変数）

Variable Dataカテゴリーには、特定アプリへの入力値および出力値が格納される変数が含まれています。C > [Variable Data]を選ぶと表示されるメニュー項目は、アプリ名を表します。

Variable Data > Statistics

このカテゴリーに含まれる変数には、Statisticsアプリを使って統計計算やグラフの描画を実行したときの、入力値や計算結果が格納されます。

Statistics > X

1変数統計計算または2変数統計計算の $x$ データに基づく値です。

メニュー項目	変数
Data Items	n
Data x Mean	$\bar{x}$
Data x Sum	$Σ x$
x-Data Sum of Squares	$Σ x^{2}$
x-Data Population Std Dev	σx
x-Data Sample Std Dev	sx
X-Data Minimum	minX
X-Data Maximum	maxX

Statistics > Y

2変数統計計算の $y$ データに基づく値です。

メニュー項目	変数
Data y Mean	$\bar{y}$
Data y Sum	$Σ y$
y-Data Sum of Squares	$Σ y^{2}$
xy-Data Products Sum	$Σ xy$
y-Data Population Std Dev	σy
y-Data Sample Std Dev	sy
Y-Data Minimum	minY
Y-Data Maximum	maxY

Statistics > Graph

下記は回帰モデル情報の各値です。

メニュー項目	変数
a Regression Coefficient	a
b Regression Coefficient	b
c Regression Coefficient	c
d Regression Coefficient	d
e Regression Coefficient	e
Correlation Coefficient	r
Coefficient of Determination	$r^{2}$
Error Mean Square	MSe

下記は1変数統計計算結果の各値です。

メニュー項目	変数
1st Quartile	$Q_{1}$
Input Data Median	Med
3rd Quartile	$Q_{3}$
Input Data Mode	Mod

Statistics > Point Coordinates

Med-Med Regression（Med-Med回帰）を実行したときの、サマリーポイント座標の各値です。

メニュー項目	変数
Summary Point Coords‎ ‎ $x_{1}$ ‎	$x_{1}$
Summary Point Coords‎ ‎ $x_{2}$ ‎	$x_{2}$
Summary Point Coords‎ ‎ $x_{3}$ ‎	$x_{3}$
Summary Point Coords‎ ‎ $y_{1}$ ‎	$y_{1}$
Summary Point Coords‎ ‎ $y_{2}$ ‎	$y_{2}$
Summary Point Coords‎ ‎ $y_{3}$ ‎	$y_{3}$

Statistics > Input

統計計算の入力値です。

メニュー項目	変数
Sample Size	n
Sample Mean	$\bar{x}$
Sample Standard Deviation	sx
Sample 1 Size	n1
Sample 2 Size	n2
Sample 1 Mean	$\bar{x}$ 1
Sample 2 Mean	$\bar{x}$ 2
Sample 1 Standard Deviation	sx1
Sample 2 Standard Deviation	sx2
Sample p Standard Deviation	sp

Statistics > Result > Test

検定計算の出力値です。

メニュー項目	変数
p	p
z	z
t	t
$χ^{2}$	$χ^{2}$
F	F
Estimated Sample Proportion	$\hat{p}$
Estim Sample 1 Proportion	$\hat{p}$ 1
Estim Sample 2 Proportion	$\hat{p}$ 2
Degree of Freedom	df
Standard Error	se
Correlation Coefficient	r
Coefficient of Determination	$r^{2}$
p Value of Factor A	pa
F Value of Factor A	Fa
Factor A Degrees of Freedom	Adf
Factor A Sum of Squares	SSa
Factor A Mean Squares	MSa
p Value of Factor B	pb
F Value of Factor B	Fb
Factor B Degrees of Freedom	Bdf
Factor B Sum of Squares	SSb
Factor B Mean Squares	MSb
Factor AB p Value	pab
Factor AB F Value	Fab
Factor AB Deg of Freedom	ABdf
Factor AB Sum of Squares	SSab
Factor AB Mean Squares	MSab
Error Degrees of Freedom	Edf
Error Sum of Squares	SSe
Error Mean Square	MSe

Statistics > Result > Confidence Interval

信頼区間計算の出力値です。

メニュー項目	変数
Confidence Int Lower Limit	Lower
Confidence Int Upper Limit	Upper
Estimated Sample Proportion	$\hat{p}$
Estim Sample 1 Proportion	$\hat{p}$ 1
Estim Sample 2 Proportion	$\hat{p}$ 2
Degree of Freedom	df

Variable Data > Distribution

このカテゴリーに含まれる変数には、Distributionアプリを使って分布計算を実行したときの計算結果が格納されます。

メニュー項目	変数
p	p
x Inverse	xInv
x1 Inverse	x1InvN
x2 Inverse	x2InvN
Normal Cumulative Dist Lower	zLow
Normal Cumulative Dist Upper	zUp
t Cumulative Dist Lower	tLow
t Cumulative Dist Upper	tUp

Variable Data > Table

メニュー項目	変数	解説
Function Table Result	F Result	Graph&TableアプリのTableタブの内容を、行列形式で出力します。

Variable Data > Recursion

メニュー項目	変数	解説
Recursion Table Result	R Result	RecursionアプリのTableタブの内容を、行列形式で出力します。

Variable Data > Equation

このカテゴリーに含まれる変数には、Equationアプリを使って高次方程式または連立方程式を解いたときの、入力値や計算結果が格納されます。

メニュー項目	変数	解説
Hi-Ord Coeff	Ply Coef	高次方程式の入力係数を、行列形式で出力します。
Hi-Ord Solutions	Ply Result	高次方程式の計算結果を、行列形式で出力します。
Linear Coeffs	Sim Coef	連立方程式の入力係数を、行列形式で出力します。
Linear Solutions	Sim Result	連立方程式の計算結果を、行列形式で出力します。

All > A ～ Z

すべての関数、コマンド、アプリデータ変数のアルファベット順一覧です。詳しくは、Catalogメニュー詳細を参照してください。

All > Symbol

下記の関数や記号が含まれます。

$\sqrt[3]{}$ ()	!	∠	E‎ (Engineer Symbol)
$_{10}$ ^()	‎°‎‎ (Degrees)	:	P‎ (Engineer Symbol)
{	‎ $^{r}$ ‎ (Radians)		T‎ (Engineer Symbol)
}	‎ $^{g}$ ‎ (Gradians)	=	G‎ (Engineer Symbol)
≠	°	$	M‎ (Engineer Symbol)
<	$\sqrt{}$ ()	,	k‎ (Engineer Symbol)
>	$\sqrt[x]{}$	(	m‎ (Engineer Symbol)
≤	$^{-1}$	)	‎ $μ$ ‎ (Engineer Symbol)
≥	$^{2}$	[	n‎ (Engineer Symbol)
”	＾	]	p‎ (Engineer Symbol)
~		‎‎ (Sci Notation)	f‎ (Engineer Symbol)
$π$	-	‎‎ (Sci Notation)

Catalogメニュー詳細

入力履歴を利用する

入力履歴をピン留めする

カテゴリー別項目一覧

Function Analysis（解析関数）

1st Derivative‎ (d/dx) d/dx(,)

2nd Derivative‎ (d2/dx2) d2/dx2(,)

Integration‎ (∫)‎ ∫(,,)

Summation‎ (Σ) Σ(,,,)

Solve Equation (SolveN) SolveN()

Solve Equation (Solve) Solve(,)

Remainder of Integer‎÷‎Integer Rmdr

Integer Part of Int‎÷‎Int Int÷

Simplification I﻿Simp

Function Minimum FMin(,,)

Function Maximum FMax(,,)

Probability（確率）

Factorial (!)‎ !

Permutation‎ (P) P

Combination‎ (C) C

Random Number (0 to 1) Ran#

Random Integer (n to m) RanInt#(,)

Random Number (Normal) RanNorm#(,)

Random Number (Binomial) RanBin#(,)

Random Num (0 to 1) to List RanList#()

Random Sample from List RanSamp#(,)

Numeric Calc（数値計算）

GCD GCD(,)

LCM LCM(,)

Absolute Value Abs()

Integer Part Int()

Fraction Part Frac()

Round Off Rnd

Largest Integer Intg()

Round Internal RndFix()

Division Remainder MOD(,)

Remainder Exponentiation MOD_Exp(,,)

Vector（ベクトル計算）

Vector Vct

Dot Product DotP(,)

Cross Product CrossP(,)

‎2-Vector Angle Angle(,)

Unit Vector UnitV()

Vector Norm Norm()

Matrix（行列計算）

Matrix Mat

Inverse Matrix -1

Determinant Det()

Matrix Transpose Trn()

Matrix Identity Identity()

Row Echelon Form Ref()

Reduced Row Echelon Form Rref()

Matrix Augment Augment(,)

Fill Matrix Fill(,)

Dimensions Dim()

Complex Number（複素数計算）

Norm of a Complex Number Abs()

Argument Arg()

Complex Conjugate Conjg()

Real Part ReP()

Imaginary Part ImP()

Ir∠θ Ir∠θ

Ia+bi Ia+bi

Statistics（統計計算）

{} {}

List List

Dimensions Dim()

Fill List Fill(,)

Generate Sequence Seq(,,,,)

Minimum Min()

Maximum Max()

Mean Mean()

Median Median()

Combine Lists Augment(,)

Sum of List Elements Sum()

List Product Prod()

Cumulative Frequency Cuml()

Data Percentages Percent()

List Data Diff ΔList

Estimated x-Data x^Estimated y-Data y^

2nd Derivative‎ (d²/dx²) d²/dx²(,)

Simplification ISimp

Inverse Matrix ^-1

Ia+b $i$ Ia+b $i$

Estimated x-Data $\hat{x}$
Estimated y-Data $\hat{y}$

Population Variance Variance_ $σ^{2}$ ()

Normal Probability P(t) P()
Normal Probability‎ Q(t) Q()
Normal Probability R(t) R()

‎ $χ^{2}$ ‎ Probability Density ChiPD(,)

‎ $χ^{2}$ ‎ Cumulative Distribution ChiCD(,,)

Inverse‎ ‎ $χ^{2}$ Cumulative Dist InvChiCD(,)

Radians $^{r}$

Gradians $^{g}$